Рассчитаем параметры линейной функции
Параметры a и b линейной регрессии  рассчитываем в результате решения системы нормальных уравнений относительно a и b. рассчитываем в результате решения системы нормальных уравнений относительно a и b.
 , (2.1) , (2.1)
Таблица 1– Вспомогательная расчетная таблица
| Номер региона
|

|
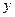
|

|

|

|

|

|

| |
| 4, 5
| 68, 8
| 309, 6
| 20, 25
| 4733, 44
| 67, 1
| 1, 7
| 2, 47
| |
| 5, 9
| 58, 3
| 343, 97
| 34, 81
| 3398, 89
| 59, 3
| –1, 0
| 1, 72
| |
| 5, 7
| 62, 6
| 356, 82
| 32, 49
| 3918, 76
| 60, 4
| 2, 2
| 0, 51
| |
| 7, 2
| 52, 1
| 375, 12
| 51, 84
| 2714, 41
| 52, 2
| –0, 1
| 0, 19
| |
| 6, 2
| 54, 5
| 337, 90
| 38, 44
| 2970, 25
| 57, 7
| –3, 2
| 5, 87
| |
| 6, 0
| 57, 1
| 342, 60
| 36, 00
| 3260, 41
| 58, 8
| –1, 7
| 2, 98
| |
| 7, 8
| 51, 0
| 397, 80
| 60, 84
| 2601, 00
| 48, 9
| 2, 1
| 4, 12
| 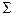
| 43, 3
| 404, 4
| 2463, 81
| 274, 67
| 23597, 16
| 404, 4
|
| 20, 86
| | Среднее значение
|
6, 186
|
57, 77
|
351, 97
|
39, 24
|
3371, 02
|
–
|
–
|
–
|
По исходным данным рассчитаем     
Система нормальных уравнений составит:
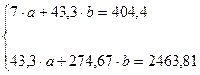
Решим ее методом определителей: определитель системы  равен: равен:
  , (2.2) , (2.2)
  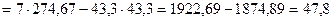
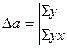  , (2.3) , (2.3)
  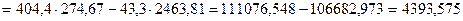
 , (2.4) , (2.4)
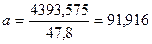
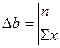  , (2.5) , (2.5)
  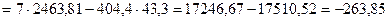
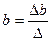 , (2.6) , (2.6)
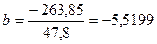
Получаем уравнение регрессии:
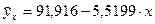
Величина коэффициента регрессии  означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5, 5 %–х пункта. означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5, 5 %–х пункта.
Чтобы рассчитать ошибку аппроксимации, найдем расчетные значения  , подставляя в уравнение регрессии соответствующие значения , подставляя в уравнение регрессии соответствующие значения  . .
2. Найдем показатели тесноты связи линейной модели:
Линейный коэффициент корреляции равен:
 , (2.7) , (2.7)
 , (2.8) , (2.8)
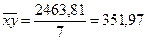
 , (2.9) , (2.9)
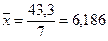
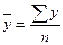 , (2.10) , (2.10)
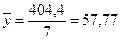
 , (2.11) , (2.11)
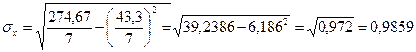
 , (2.12) , (2.12)

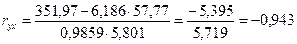
Вывод: связь между признаками очень высокая обратная, так 0, 9 <  < 0, 99 < 0, 99

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|
Методы анализа финансово-хозяйственной деятельности предприятия
Содержанием анализа финансово-хозяйственной деятельности предприятия является глубокое и всестороннее изучение экономической информации о функционировании анализируемого субъекта хозяйствования с целью принятия оптимальных управленческих...
Образование соседних чисел Фрагмент:
Программная задача: показать образование числа 4 и числа 3 друг из друга...
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|
Оценка качества Анализ документации. Имеющийся рецепт, паспорт письменного контроля и номер лекарственной формы соответствуют друг другу. Ингредиенты совместимы, расчеты сделаны верно, паспорт письменного контроля выписан верно. Правильность упаковки и оформления....
БИОХИМИЯ ТКАНЕЙ ЗУБА В составе зуба выделяют минерализованные и неминерализованные ткани...
Типология суицида. Феномен суицида (самоубийство или попытка самоубийства) чаще всего связывается с представлением о психологическом кризисе личности...
|
|

 рассчитываем в результате решения системы нормальных уравнений относительно a и b.
рассчитываем в результате решения системы нормальных уравнений относительно a и b. , (2.1)
, (2.1)
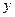






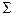





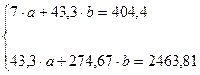
 равен:
равен:
 , (2.2)
, (2.2)

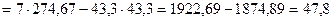
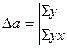

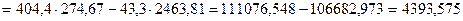
 , (2.4)
, (2.4)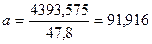
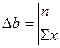
 , (2.5)
, (2.5)

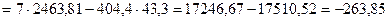
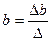 , (2.6)
, (2.6)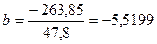
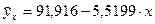
 означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5, 5 %–х пункта.
означает, что с ростом заработной платы на 1 тыс. руб. доля расходов на покупку продовольственных товаров снижается в среднем на 5, 5 %–х пункта. , подставляя в уравнение регрессии соответствующие значения
, подставляя в уравнение регрессии соответствующие значения  .
. , (2.7)
, (2.7) , (2.8)
, (2.8)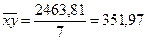
 , (2.9)
, (2.9)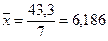
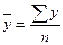 , (2.10)
, (2.10)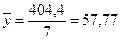
 , (2.11)
, (2.11)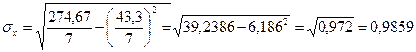
 , (2.12)
, (2.12)
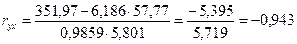
 < 0, 99
< 0, 99


