Задача №3. По 12 предприятиям отрасли изучается зависимость прибыли (тыс
По 12 предприятиям отрасли изучается зависимость прибыли (тыс. руб.) у от выработки продукции на одного человека (единиц) х по следующим данным: Таблица 1– Исходные данные
Требуется: 1. Построить линейное уравнение парной регрессии у = f(x). 2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. 3.Оценить статистическую значимость параметров регрессии и корреляции. 4. Дать точечный и интервальный прогноз прибыли с вероятностью 0, 95, принимая уровень выработки равным 92 единицам. Решение: 1. Для расчета параметров уравнения линейной регрессии строим таблицу 2. Таблица 2– Расчетная таблица
Рассчитаем параметры
Получаем уравнение регрессии:
С увеличением выработки на 1 единицу прибыль возрастает в среднем на 0, 92 тыс. руб. 2. Тесноту линейной связи измеряет коэффициент корреляции:
Коэффициент корреляции можно также рассчитать по формуле:
Величина коэффициента корреляции означает достаточно тесную связь рассматриваемых признаков. Коэффициент детерминации Качество модели оценивается как хорошее, так как 3. Оценку статистической значимости параметров регрессии проведем с помощью Выдвигаем гипотезу Но о статистически незначимых отличиях от нуля значений показателей:
Определим случайные ошибки параметров
где
Далее вычисляем значения критерия Стьюдента:
Фактические значения Рассчитаем доверительный интервал для a и b, для чего определим предельную ошибку для каждого параметра:
Доверительные интервалы:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если примем прогнозное значение выработки
Чтобы получить интервальный прогноз, найдем стандартную ошибку предсказываемого значения прибыли
Предельная ошибка прогнозируемой прибыли составит:
Доверительный интервал прогнозируемой прибыли составит:
то есть при выработке, равной 92 единицы, получим значение прибыли не меньше чем
|


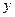

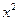







 и
и  по формулам:
по формулам: , (2.29)
, (2.29)
 , (2.30)
, (2.30)

 , (2.31)
, (2.31) , (2.7)
, (2.7) , (2.8)
, (2.8)
 , (2.9)
, (2.9)
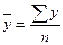 , (2.10)
, (2.10)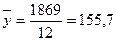
 , (2.11)
, (2.11)
 , (2.12)
, (2.12)

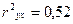 показывает, что 52 % вариации прибыли связано с вариацией выработки продукции на одного работника.
показывает, что 52 % вариации прибыли связано с вариацией выработки продукции на одного работника. - статистики Стьюдента и вычислим доверительные интервалы для каждого из показателей.
- статистики Стьюдента и вычислим доверительные интервалы для каждого из показателей.
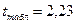 для числа степеней свободы
для числа степеней свободы 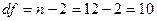
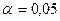
 ,
, 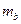 и коэффициента корреляции
и коэффициента корреляции 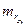 :
: , (2.32)
, (2.32) – стандартная ошибка регрессии, определяемая как
– стандартная ошибка регрессии, определяемая как , (2.33)
, (2.33)

 , (2.34)
, (2.34)
 , (2.35)
, (2.35)
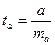 , (2.36)
, (2.36)
 , (2.37)
, (2.37)
 , (2.38)
, (2.38)
 :
:  . Поэтому гипотеза Но отклоняется, то есть
. Поэтому гипотеза Но отклоняется, то есть  отличаются от нуля не случайно и их значения статистически значимы.
отличаются от нуля не случайно и их значения статистически значимы. , (2.39)
, (2.39)
 , (2.40)
, (2.40)
 , (2.41)
, (2.41)
 , (2.42)
, (2.42)
 , (2.43)
, (2.43)
 , (2.44)
, (2.44)
 , (2.45)
, (2.45)
 , (2.46)
, (2.46)
 параметры
параметры  , то точечный прогноз прибыли составит:
, то точечный прогноз прибыли составит: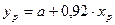 , (2.47)
, (2.47) тыс. руб.
тыс. руб. :
: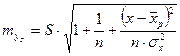 , (2.48)
, (2.48) тыс. руб.
тыс. руб. , (2.49)
, (2.49) тыс. руб.
тыс. руб.
 тыс. руб., и не больше чем
тыс. руб., и не больше чем  тыс. руб.
тыс. руб.


