Степенная модель
Регрессия в виде степенной функции имеет вид:
 , (2.23) , (2.23)
Для оценки параметры a и b, линеаризуем модель путем логарифмирования:
 , (2.24) , (2.24)
Обозначим  ; ;  ; ; 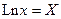
Тогда получим:
 , (2.25) , (2.25)
Применяя метод МНК (метод наименьших квадратов), получаем систему нормальных уравнений:
 , (2.26) , (2.26)
Для расчета параметров составим таблицу 2.
По исходным данным рассчитаем  , ,  , ,  , , 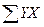
Система нормальных уравнений составит:
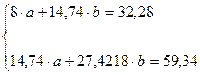
Решим ее методом определителей: определитель системы  равен: равен:
 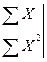 , (2.27) , (2.27)
Таблица 3 – Вспомогательная расчетная таблица
| Номер региона
|

|
|

|

|

|

|

|

|

|

|

|

| |
| 4, 5
| 68, 8
| 1, 50
| 4, 23
| 6, 36
| 2, 2622
| 17, 9031
| 4, 22
| 68, 28
| 0, 52
| 0, 27
| 0, 756
| |
| 5, 9
| 58, 3
| 1, 77
| 4, 07
| 7, 22
| 3, 1505
| 16, 5291
| 4, 07
| 58, 70
| –0, 40
| 0, 16
| 0, 686
| |
| 5, 7
| 62, 6
| 1, 74
| 4, 14
| 7, 20
| 3, 0292
| 17, 1128
| 4, 09
| 59, 84
| 2, 76
| 7, 62
| 4, 430
| |
| 7, 2
| 52, 1
| 1, 97
| 3, 95
| 7, 80
| 3, 8970
| 15, 6275
| 3, 96
| 52, 52
| – 0, 42
| 0, 18
| 0, 806
| |
| 6, 2
| 54, 5
| 1, 82
| 4, 00
| 7, 29
| 3, 3290
| 15, 9856
| 4, 04
| 57, 09
| – 2, 59
| 6, 73
| 4, 752
| |
| 6, 0
| 57, 1
| 1, 79
| 4, 04
| 7, 25
| 3, 2104
| 16, 3604
| 4, 06
| 58, 15
| –1, 05
| 1, 10
| 1, 839
| |
| 7, 8
| 51, 0
| 2, 05
| 3, 93
| 8, 08
| 4, 2194
| 15, 4593
| 3, 92
| 50, 23
| 0, 77
| 0, 60
| 1, 510
| |
| 8, 0
| 50, 1
| 2, 08
| 3, 91
| 8, 14
| 4, 3241
| 15, 3196
| 3, 90
| 49, 52
| 0, 58
| 0, 34
| 1, 158
| 
| 51, 3
| 454, 5
| 14, 74
| 32, 28
| 59, 34
| 27, 4218
| 130, 2974
| 32, 28
| 454, 33
| 0, 17
| 17, 00
| 15, 937
| | В среднем
| 6, 4125
| 56, 8125
| 1, 84
| 4, 03
| 7, 42
| 3, 4277
| 16, 2872
|
|
|
|
| 1, 992
|
  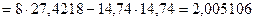
 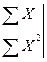 , (2.28) , (2.28)
 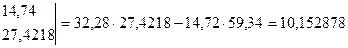
 , (2.29) , (2.29)
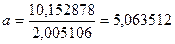
  , (2.30) , (2.30)
  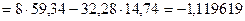
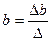 , (2.6) , (2.6)
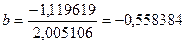
Получаем уравнение регрессии:
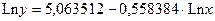
Выполнив потенцирование, получим: 
Теоретические значения зависимой переменной  получим, подставив в уравнение получим, подставив в уравнение 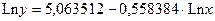 значения х и потенцируя значения значения х и потенцируя значения  . .
Для оценки тесноты связи найдем индекс корреляции:
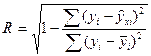
Остаточная сумма квадратов составит:
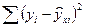
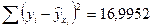
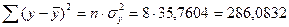
Следовательно, индекс корреляции составит:
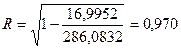
Коэффициент детерминации для уравнения степенной функции равен:
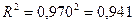
 критерий Фишера будет равен: критерий Фишера будет равен:
 , (2.22) , (2.22)
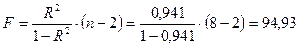
Табличное значение  критерий Фишера при числе степеней свободы 1 и 6 и уровне значимости 0, 05 составит: критерий Фишера при числе степеней свободы 1 и 6 и уровне значимости 0, 05 составит:  , то есть фактическое значение , то есть фактическое значение  критерия превышает табличное, и можно сделать вывод, что уравнение регрессии статистически значимо. критерия превышает табличное, и можно сделать вывод, что уравнение регрессии статистически значимо.
Ошибки аппроксимации для каждого наблюдения определяются как
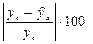 %, (2.14) %, (2.14)
Средняя ошибка аппроксимации  находится, как средняя арифметическая простая из индивидуальных ошибок: находится, как средняя арифметическая простая из индивидуальных ошибок:
 % %
Ошибка аппроксимации показывает соответствие расчетных  и фактических и фактических  данных. данных.
Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одной таблице.
Таблица 4– Итоговая таблица
| Уравнение регрессии
| Коэффициент детерминации
|  критерий Фишера критерий Фишера
| Средняя ошибка аппроксимации 
| 
| 0, 896
| 
| 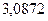 % %
| 
| 
| 
|  % %
| 
| 
| 
| 1, 992 %
|
Наилучшей моделью является гиперболическая модель, для которой значение  достаточно высокое, а ошибка аппроксимации – наименьшая. достаточно высокое, а ошибка аппроксимации – наименьшая.

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|
Философские школы эпохи эллинизма (неоплатонизм, эпикуреизм, стоицизм, скептицизм). Эпоха эллинизма со времени походов Александра Македонского, в результате которых была образована гигантская империя от Индии на востоке до Греции и Македонии на западе...
Демографияда "Демографиялық жарылыс" дегеніміз не? Демография (грекше демос — халық) — халықтың құрылымын...
Субъективные признаки контрабанды огнестрельного оружия или его основных частей
Переходя к рассмотрению субъективной стороны контрабанды, остановимся на теоретическом понятии субъективной стороны состава преступления...
|
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста.
Врачи-хирурги выяснили...
ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИЗНОС ДЕТАЛЕЙ, И МЕТОДЫ СНИЖЕНИИ СКОРОСТИ ИЗНАШИВАНИЯ Кроме названных причин разрушений и износов, знание которых можно использовать в системе технического обслуживания и ремонта машин для повышения их долговечности, немаловажное значение имеют знания о причинах разрушения деталей в результате старения...
|
|

 , (2.23)
, (2.23) , (2.24)
, (2.24) ;
;  ;
; 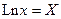
 , (2.25)
, (2.25) , (2.26)
, (2.26) ,
,  ,
,  ,
, 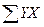
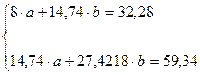
 равен:
равен:
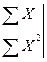 , (2.27)
, (2.27)
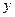










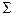


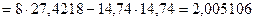


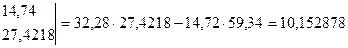
 , (2.29)
, (2.29)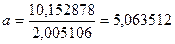

 , (2.30)
, (2.30)

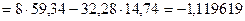
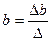 , (2.6)
, (2.6)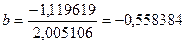
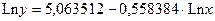

 получим, подставив в уравнение
получим, подставив в уравнение  .
.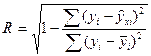
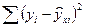
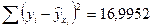
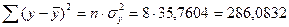
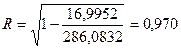
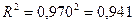
 критерий Фишера будет равен:
критерий Фишера будет равен: , (2.22)
, (2.22)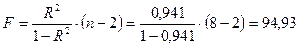
 , то есть фактическое значение
, то есть фактическое значение 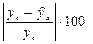 %, (2.14)
%, (2.14) находится, как средняя арифметическая простая из индивидуальных ошибок:
находится, как средняя арифметическая простая из индивидуальных ошибок: %
% и фактических
и фактических  данных.
данных.

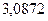 %
%



 %
%



 достаточно высокое, а ошибка аппроксимации – наименьшая.
достаточно высокое, а ошибка аппроксимации – наименьшая.


