Частный F - критерий Фишера оценивает статистическую целесообразность включения фактора 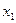 в модель после того, как в нее включен фактор
в модель после того, как в нее включен фактор 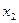 .
.
Частный F - критерий Фишер строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), рассчитанной по модели с включенными факторами 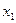 и
и 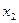 :
:
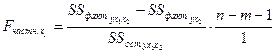 , (3.21)
, (3.21)
Результаты дисперсионного анализа представлены в таблице 3.
Таблица 3– Дисперсионный анализ
Вариация результата, 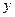
| Число степеней свободы
| Сумма квадратов отклонений
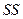 
| Дисперсия на одну степень свободы, 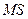
| 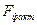
| 
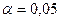
|
| Общая
| 
| 19945, 9
| –
| –
| –
|
Факторная
в том числе:
– за счет 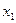 –за счет дополнительно
включенного
–за счет дополнительно
включенного 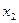
| 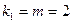
| 11918, 3
5127, 1
6791, 2
| 5959, 15
5127, 1
6791, 2
| 12, 62
1, 73
14, 38
| 3, 59
4, 45
4, 45
|
| Остаточная
| 
| 8027, 6
| 472, 21
| –
| –
|
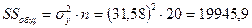
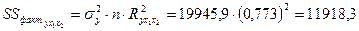
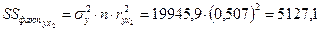
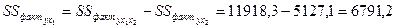
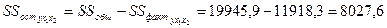
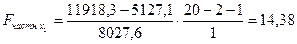
Включение фактора 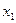 после фактора
после фактора 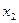 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, то есть следствием дополнительного включения в модель систематически действующего фактора
оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, то есть следствием дополнительного включения в модель систематически действующего фактора 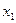 , так как
, так как 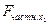 =14, 38 >
=14, 38 >  =4, 45.
=4, 45.
Аналогично проверим целесообразность включения в модель дополнительного фактора 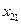 после включенного ранее фактора
после включенного ранее фактора 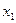 .
.
Расчет выполним с использованием показателей тесноты связи  ,
, 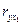 :
:
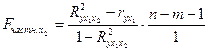 , (3.22)
, (3.22)
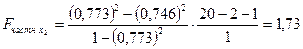
В силу того, что  , включение
, включение  оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы несуществен и статистически незначим, то есть влияние
оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы несуществен и статистически незначим, то есть влияние  не является устойчивым, систематическим; можно было ограничиться построением линейного уравнения парной регрессии
не является устойчивым, систематическим; можно было ограничиться построением линейного уравнения парной регрессии 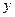 от
от  .
.

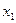 в модель после того, как в нее включен фактор
в модель после того, как в нее включен фактор 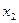 .
.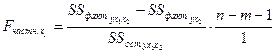 , (3.21)
, (3.21)
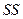

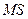
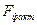

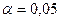

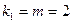

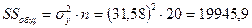
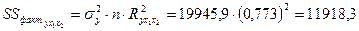
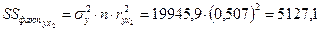
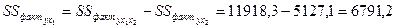
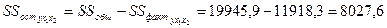
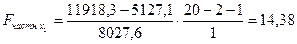
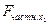 =14, 38 >
=14, 38 > 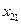 после включенного ранее фактора
после включенного ранее фактора  ,
, 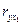 :
: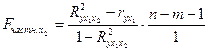 , (3.22)
, (3.22)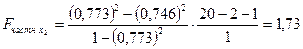
 , включение
, включение  оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы несуществен и статистически незначим, то есть влияние
оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы несуществен и статистически незначим, то есть влияние  .
.


