Третье уравнение
Н: эндогенных переменных – 2 (y 2, y 3), отсутствующих экзогенных – 1 (x 2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в третьем уравнении отсутствуют y 1 и x 2. Построим матрицу из коэффициентов при них в других уравнениях системы:
Det A = -l× a 22 - b 21 × 0 ¹ 0. Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов. 2. Вычислим структурные коэффициенты модели: 1) из третьего уравнения приведенной формы выразим х 2 (так как его нет в первом уравнении структурной формы):
Данное выражение содержит переменные y 3, x 1 и x 3, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x 2 в первое уравнение приведенной формы модели (ПФМ):
2) во втором уравнении СФМ нет переменных x 1 и x 3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа: Первый этап: выразим x 1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:
Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x 3, которого нет в СФМ. Выразим x 3 из третьего уравнения ПФМ:
Подставим его в выражение x 1:
Второй этап: аналогично, чтобы выразить x 3 через искомые y 1, y 3, и x 2, заменим в выражении x 3 значение x 1 на полученное из первого уравнения ПФМ:
Следовательно,
Подставим полученные x 1 и x 3 во второе уравнение ПФМ:
3) из второго уравнения ПФМ выразим x 2, так как его нет в третьем уравнении СФМ:
Подставим полученное выражение в третье уравнение ПФМ:
Таким образом, СФМ примет вид
|

 .
. Þ
Þ – первое уравнение СФМ:
– первое уравнение СФМ: .
. .
.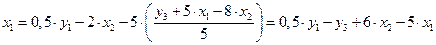 ;
; .
.
 .
.
 – второе уравнение СФМ.
– второе уравнение СФМ. .
.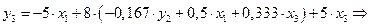
 – третье уравнение СФМ.
– третье уравнение СФМ.



