Пример 1. МОДЕЛЬ С АДДИТИВНОЙ КОМПОНЕНТОЙ
Приведены данные о количестве продукции, проданной компанией в течение последних 13 кварталов.
Требуется: 1. Построить аддитивную модель временного ряда. 2. Сделать прогноз на 2 квартала вперед. Решение. 1. Проанализируем данные и попробуем обнаружить тенденцию. Если устойчивая тенденция действительно существует, то построенную модель можно будет использовать для прогнозирования объема продаж в следующих кварталах. Для этого построим график временного ряда (см. рис.).
Из графика следует, что возможен возрастающий тренд, содержащий сезонные колебания. Так объемы продаж в зимний период (1 и 4) значительно выше, чем в летний (2 и 3). Сезонная компонента практически не изменилась за последние три года. Тренд показывает, что в среднем объем продаж возрос с 240 тыс. шт. в 2003 г. до 480 тыс. шт. в 2006 г., однако увеличение сезонных колебаний не наблюдалось. Этот факт свидетельствует в пользу модели с аддитивной компонентой
2. Расчет сезонной компоненты. Для исключения влияния сезонной компоненты используют метод скользящей средней, суть которого заключается в нахождении среднего арифметического значения параметра за m моментов времени
Для рассмотренных данных об объемах продаж проведем следующие расчеты. 1. Производя скольжение по значениям квартальных продаж из колонки 2, вычислим сумму продаж за каждые четыре квартала и внесем ее в колонку 3 табл. 1. 2. Вычислим скользящую среднюю за каждые 4 квартала (колонка 4). 3. Поскольку усредненные данные, внесенные в колонку 3, относятся не к конкретному кварталу, а к моменту времени между двумя кварталами (например, между апрелем-июнем и июлем-сентябрем 2003 г.), то необходимо получить центрированную скользящую среднюю для каждой пары значений из колонки 4. Полученные значения относятся к конкретным кварталам, начиная с июля-сентября 2003 года, их вносят в колонку 5. Таким образом, величины из колонки 5 являются десезонализированными средними значениями за квартал. 4. Сезонную компоненту, содержащую остаток, рассчитывают по формуле 5. Используя данные за все годы, вычисляют среднее значение для каждого квартала, что позволит уменьшить значения ошибок (табл. 2). 6. Средние оценки сезонной компоненты корректируются, путем увеличения или уменьшения некоторых из них на одно и то же число, таким образом, чтобы их общая сумма была равна 0. Корректирующий фактор рассчитывают следующим образом: сумма оценок сезонных компонент делится на 4. Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Например, если в качестве сезонов рассматриваются не кварталы, а дни недели, то устранения влияния сезонной компоненты рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, т.е. в четверг. Поэтому в этом случае необходимость в центрировании отпадает. 3. Десезонализация данных при расчете тренда. Десезонализация исходных данных заключается в вычитании скорректированных сезонных компонент (последняя строка табл. 2) из фактических значений данных за каждый квартал, т.е. Нанесем значения новых оценок тренда из колонки 4 на график исходных данных, что еще раз подтвердит существование явного линейного тренда. Определим уравнение линии тренда методом наименьших квадратов
Таблица 1
Таблица 2
Таблица 3
4. Расчет ошибок Из (1) следует, что величина ошибки равна
Значение T найдем из уравнения (2), а S из табл. 2. Результаты расчета представлены в табл. 4. Таблица 4
Столбец 5 можно использовать при расчете среднего абсолютного отклонения MAD (mean absolute deviation) и средней квадратической ошибки MSE (mean square error):
где В нашем случае ошибки достаточно малы и составляют от 0, 2% до 2, 2%. Тенденция, выявленная по фактическим данным, достаточно устойчива и позволяет получить хорошие краткосрочные прогнозы. 5. Прогнозирование по аддитивной модели. Прогнозные значения рассчитываются по формуле
где x – номер квартала, на который дается прогноз, T – значение тренда, рассчитанное по (2), S (x) – сезонная компонента, составляющая в январе-марте 42, 6, в апреле-июне – 20, 7, в июле-сентябре – 62, 0, в октябре-декабре – 40, 1. Например, прогноз на апрель-июнь 2006 г. (x = 14) имеет вид
Можно предположить, что ошибка прогноза будет приблизительно 0, 3-2, 2% в соответствии с рассчитанными ошибками модели, но чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза.
|


 . (1)
. (1) .
. и вносят в колонку 6.
и вносят в колонку 6. (табл. 3).
(табл. 3). . (2)
. (2)

 .
. и
и 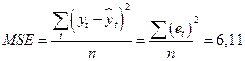 .
. и
и  – это фактическое и прогнозное значение в момент времени t.
– это фактическое и прогнозное значение в момент времени t. (тыс. шт. за квартал),
(тыс. шт. за квартал), ,
, тыс. шт.
тыс. шт.


