Построение степенной модели парной регрессии
Уравнение степенной модели имеет вид: 
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
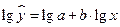 . .
|
| Факт
| 
| Переменная
| 
| |
| 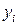
|
| 
|
| |
| 64, 0
| 1, 806
|
| 1, 806
| |
| 56, 0
| 1, 748
|
| 1, 833
| |
| 52, 0
| 1, 716
|
| 1, 914
| |
| 48, 0
| 1, 681
|
| 1, 881
| |
| 50, 0
| 1, 699
|
| 1, 924
| |
| 46, 0
| 1, 663
|
| 1, 982
| |
| 38, 0
| 1, 580
|
| 2, 000
| |
|
| 11, 893
|
| 13, 340
| | Средн. знач.
| 50, 5714
| 1, 699
| 81, 429
| 1, 906
| Обозначим 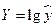 , ,  , ,  . .
Тогда уравнение примет вид:
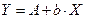 – линейное уравнение регрессии. – линейное уравнение регрессии. 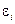
Рассчитаем его параметры, используя данные таблицы 2.
Таблица 2
|
| y
| Y
| x
| X
| Y× X
| X 2
| 
| 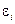
| 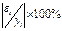
| 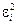
| |
|
| 1, 806
|
| 1, 806
| 3, 262
| 3, 262
| 61, 294
| 2, 706
| 4, 23
| 7, 32
| |
|
| 1, 748
|
| 1, 832
| 3, 203
| 3, 358
| 58, 066
| –2, 066
| 3, 69
| 4, 27
| |
|
| 1, 716
|
| 1, 913
| 3, 284
| 3, 662
| 49, 133
| 2, 867
| 5, 51
| 8, 22
| |
|
| 1, 681
|
| 1, 880
| 3, 162
| 3, 537
| 52, 580
| –4, 580
| 9, 54
| 20, 97
| |
|
| 1, 699
|
| 1, 924
| 3, 269
| 3, 702
| 48, 088
| 1, 912
| 3, 82
| 3, 65
| |
|
| 1, 662
|
| 1, 982
| 3, 296
| 3, 929
| 42, 686
| 3, 314
| 7, 20
| 10, 98
| |
|
| 1, 579
|
| 2, 000
| 3, 159
| 4, 000
| 41, 159
| –3, 159
| 8, 31
| 9, 98
| | Итого
|
| 11, 893
|
| 13, 339
| 22, 637
| 25, 452
|
| 0, 51
| 42, 32
| 65, 40
| 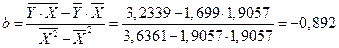 , ,
 . .
Уравнение регрессии будет иметь вид:
 . .
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
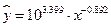 . .
Получим уравнение степенной модели регрессии:
 . .
Определим индекс корреляции:
 . .
Связь между показателем y и фактором x можно считать достаточно сильной.
Коэффициент детерминации:
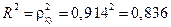 . .
Вариация результата y (объема выпуска продукции) на 83, 6 % объясняется вариацией фактора x (объемом капиталовложений).
Рассчитаем F -критерий Фишера:
 . .
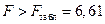 для a = 0, 05; для a = 0, 05;  , ,  . .
Уравнение регрессии с вероятностью 0, 95 в целом статистически значимое, т. к.  . .
Средняя относительная ошибка
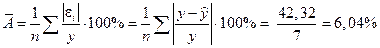 . .
В среднем расчетные значения  для степенной модели отличаются от фактических значений на 6, 04%. для степенной модели отличаются от фактических значений на 6, 04%.

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИЗНОС ДЕТАЛЕЙ, И МЕТОДЫ СНИЖЕНИИ СКОРОСТИ ИЗНАШИВАНИЯ Кроме названных причин разрушений и износов, знание которых можно использовать в системе технического обслуживания и ремонта машин для повышения их долговечности, немаловажное значение имеют знания о причинах разрушения деталей в результате старения...
Различие эмпиризма и рационализма Родоначальником эмпиризма стал английский философ Ф. Бэкон. Основной тезис эмпиризма гласит: в разуме нет ничего такого...
Индекс гингивита (PMA) (Schour, Massler, 1948) Для оценки тяжести гингивита (а в последующем и регистрации динамики процесса) используют папиллярно-маргинально-альвеолярный индекс (РМА)...
|
Понятие и структура педагогической техники Педагогическая техника представляет собой важнейший инструмент педагогической технологии, поскольку обеспечивает учителю и воспитателю возможность добиться гармонии между содержанием профессиональной деятельности и ее внешним проявлением...
Репродуктивное здоровье, как составляющая часть здоровья человека и общества
Репродуктивное здоровье – это состояние полного физического, умственного и социального благополучия при отсутствии заболеваний репродуктивной системы на всех этапах жизни человека...
Случайной величины Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) – первую производную от функции распределения F(x):
Понятие плотность распределения вероятностей случайной величины Х для дискретной величины неприменима...
|
|


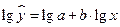 .
.

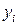

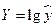 ,
,  ,
,  .
.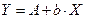 – линейное уравнение регрессии.
– линейное уравнение регрессии. 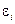

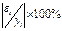
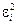
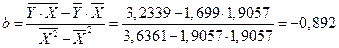 ,
, .
. .
.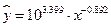 .
. .
. .
.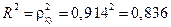 .
. .
.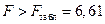 для a = 0, 05;
для a = 0, 05;  ,
,  .
. .
.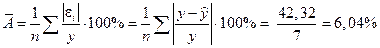 .
. для степенной модели отличаются от фактических значений на 6, 04%.
для степенной модели отличаются от фактических значений на 6, 04%.


