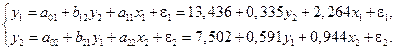Сверхиндетифицируемые
Для того чтобы СФМ была идентифицируема, необходимо чтобы каждое уравнение системы было идентифицируемо. В этом случае число параметров СФМ равно числу параметров приведенной формы. Если хотя бы одно уравнение СФМ неидентифицируемо, то вся модель считается неидентифицируемой. В этом случае число коэффициентов приведенной формы модели меньше, чем число коэффициентов СФМ. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае можно получить два и более значений одного структурного коэффициента на основе коэффициентов приведенной формы модели. В сверхидентифицируемой модели хотя бы одно уравнение сверхидентифицируемо, а остальные уравнения идентифицируемы. Если обозначить число эндогенных переменных в i -том уравнении СФМ через Н, а число предопределенных переменных, которые содержатся в системе, но не входят в данное уравнение через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила: если D+1 < H – уравнение неидентифицируемо; если D+1 = H – уравнение идентифицируемо; если D+1 > H – уравнение сверхидентифицируемо. Счетное правило является необходимым, но не достаточным условием идентификации. Кроме этого правила для идентифицируемости уравнения должно выполняться дополнительное условие. Отметим в системе эндогенные и экзогенные переменные, отсутствующие в рассматриваемом уравнении, но присутствующие в системе. Из коэффициентов при этих переменных в других уравнениях составим матрицу. При этом, если переменная стоит в левой части уравнения, то коэффициент надо брать с обратным знаком. Если определитель полученной матрицы не равен нулю, а ранг не меньше, чем количество эндогенных переменных в системе без одного, то достаточное условие индетификации для данного уравнения выполнено. Проверим каждое уравнение системы на выполнение неоходимого и достаточного условия идентификации. В первом уравнении три эндогенных переменных: Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Таблица 1 Матрица, составленная из коэффициентов при переменных
Во втором уравнении две эндогенные переменные: Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Таблица 2 Матрица, составленная из коэффициентов при переменных
Определитель представленной в таблице 2 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо. В третьем уравнении три эндогенные переменные: Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Таблица 3 Матрица, составленная из коэффициентов при переменных
При оценивании коэффициентов структурной модели используется ряд методов. Рассмотрим косвенный метод наименьших квадратов (КМНК), который применяется в случае точно идентифицируемой структурной модели. Пример 2. Рассмотрим КМНК на примере следующей идентифицируемой модели, содержащей две эндогенные и две экзогенные переменные:
Для построения модели мы располагаем информацией, представленной в таблице 4. Таблица 4. Фактические данные для построения модели
Структурную модель преобразуем в приведенную форму модели.
где u 1 и u 2 – случайные ошибки. Для каждого уравнения приведенной формы при расчете коэффициентов d можно применить МНК. Для упрощения расчетов можно работать с отклонениями от средних уровней Для нахождения коэффициентов
Таблица 5 Преобразованные данные для построения приведенной формы модели
Подставляя рассчитанные в таблице 5 значения сумм, получим
Решение этих уравнений дает значения d11 = 2, 822 и d12 = 0, 394. Первое уравнение приведенной формы модели примет вид
Для нахождения коэффициентов d2 k второго приведенного уравнения можно использовать следующую систему нормальных уравнений:
Подставляя рассчитанные в таблице 5 значения сумм, получим
Решение этих уравнений дает значения d21 = 1, 668 и d22 = 1, 177. Второе уравнение приведенной формы модели примет вид
Для перехода от приведенной формы к структурной форме модели найдем
Подставим это выражение в первое уравнение приведенной модели, найдем структурное уравнение
Таким образом, b 12 = 0, 335; a 11 = 2, 264. Найдем
Подставим это выражение во второе уравнение приведенной модели, найдем структурное уравнение
Таким образом, b 21 = 0, 591; a 22 = 0, 944. Свободные члены структурной формы находим из уравнений
Окончательный вид структурной модели
Пример 3. Изучается модель вида:
Требуется: 1. Оценить следующую структурную модель на идентификацию: 2. Исходя из приведенной формы модели уравнений
найти структурные коэффициенты модели. Решение. 1. Модель имеет три эндогенные (у 1, у 2, у 3) и три экзогенные (х 1, х 2, х 3) переменные. Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.
|

 ,
,  ,
,  (H=3). В нем отсутствуют экзогенные переменные
(H=3). В нем отсутствуют экзогенные переменные  и
и  (D=2). Необходимое условие идентификации D+1=H выполнено.
(D=2). Необходимое условие идентификации D+1=H выполнено. и
и  , соответственно. В третьем уравнении эти переменные отсутствуют, т.е. коэффициенты при них равны нулю. Так как вторая строка матрицы состоит из нулей, определитель матрицы равен нулю. Значит, достаточное условие не выполнено, и первое уравнение нельзя считать идентифицируемым.
, соответственно. В третьем уравнении эти переменные отсутствуют, т.е. коэффициенты при них равны нулю. Так как вторая строка матрицы состоит из нулей, определитель матрицы равен нулю. Значит, достаточное условие не выполнено, и первое уравнение нельзя считать идентифицируемым.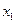 (D=1). Необходимое условие идентификации D+1=H выполнено.
(D=1). Необходимое условие идентификации D+1=H выполнено.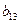


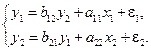

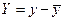 и
и  (
( и
и  – средние значения). Преобразованные таким образом данные таблицы 4 сведены в таблицу 5. Здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов
– средние значения). Преобразованные таким образом данные таблицы 4 сведены в таблицу 5. Здесь же показаны промежуточные расчеты, необходимые для определения коэффициентов  .
.

 .
.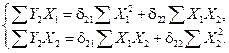

 .
. из второго уравнения приведенной формы модели
из второго уравнения приведенной формы модели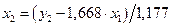 .
.
 .
. из первого уравнения приведенной формы модели
из первого уравнения приведенной формы модели .
.
 .
. ,
, .
.