Пример 2. МОДЕЛЬ С МУЛЬТИПЛИКАТИВНОЙ КОМПОНЕНТОЙ
В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения, т.е. значение сезонной компоненты увеличивается с возрастанием значений тренда. Например, рассмотрим график следующих данных об объемах продаж.
| Дата
| Объем продаж,
тыс. шт.
| Дата
| Объем продаж,
тыс. шт.
| |
|
|
|
| | Январь-март 2004
|
| Июль-сентябрь
|
| | Апрель-июнь
|
| Октябрь-декабрь
|
| | Июль-сентябрь
|
| Январь-март 2006
|
| | Октябрь-декабрь
|
| Апрель-июнь
|
| | Январь-март 2005
|
| Июль-сентябрь
|
| | Апрель-июнь
|
|
|
| 
Объем продаж этого продукта так же, как и в предыдущем примере, подвержен сезонным колебаниям, и значения его в зимний период выше, чем в летний. Однако размах вариации фактических значений относительно линии тренда постоянно возрастает. Такую ситуацию можно представить с помощью модели с мультипликативной компонентой
 . .
1. Расчет сезонной компоненты.
Отличие расчета сезонной компоненты для мультипликативной модели от аддитивной модели заключается лишь в том, что в колонку 6 вписываются коэффициенты сезонности (аналог оценок сезонной компоненты в аддитивной модели)
 . .
Сезонные коэффициенты представляют собой доли тренда, поэтому принимают, что их сумма должна равняться количеству сезонов в году, т.е. 4, а не нулю, как в аддитивной модели. Если бы в качестве сезонов рассматривались дни недели, то эта сумма равнялась бы 7. Если сумма вычисленных коэффициентов  не равна 4, то их корректируют, путем умножения соответствующей доли на не равна 4, то их корректируют, путем умножения соответствующей доли на 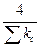 . .
Таблица 1
| Номер квартала
| Объем продаж, тыс. шт.
| Итого за четыре квартала
| Скользящая средняя за четыре квартала
| Центрирован-ная скользящая средняя
| Оценка сезонной компоненты 
| |
|
|
|
|
|
| | Январь-март 2004
|
|
|
|
|
| | Апрель-июнь
|
|
|
|
|
| | Июль-сентябрь
|
|
| 84, 5
|
| 0, 935
| | Октябрь-декабрь
|
|
| 85, 625
|
| 1, 401
| | Январь-март 2005
|
| 86, 25
| 87, 375
|
| 0, 767
| | Апрель-июнь
|
| 88, 5
| 89, 75
|
| 0, 880
| | Июль-сентябрь
|
|
| 91, 25
|
| 0, 964
| | Октябрь-декабрь
|
| 91, 5
| 91, 875
|
| 1, 415
| | Январь-март 2006
|
| 92, 25
| 92, 5
|
| 0, 746
| | Апрель-июнь
|
| 92, 75
|
|
|
| | Июль-сентябрь
|
|
|
|
|
| Таблица 2
|
| Номер квартала
| |
|
|
|
|
|
| |
|
|
| 0, 935
| 1, 401
|
| |
| 0, 767
| 0, 880
| 0, 964
| 1, 415
|
| |
| 0, 746
|
|
|
|
| | Средняя оценка сезонной компоненты
| 0, 756
| 0, 880
| 0, 950
| 1, 408
| Сумма
3, 994
| | Скорректированная сезонная компонента
| 0, 757
| 0, 881
| 0, 952
| 1, 410
| Сумма
4, 000
| 2. Десезонализация данных при расчете тренда.
Десезонализация данных производится по формуле
 . .
Таблица 3
| Номер
квартала
| Объем продаж A,
тыс. шт.
| Сезонная
компонента S
| Десезонализированный объем продаж A / S = T ´ S, тыс. шт.
| |
|
|
|
| |
|
| 0, 757
| 83, 2
| |
|
| 0, 881
| 84, 0
| |
|
| 0, 952
| 83, 0
| |
|
| 1, 410
| 85, 1
| |
|
| 0, 757
| 88, 5
| |
|
| 0, 881
| 89, 7
| |
|
| 0, 952
| 92, 4
| |
|
| 1, 410
| 92, 2
| |
|
| 0, 757
| 91, 1
| |
|
| 0, 881
| 93, 1
| |
|
| 0, 952
| 94, 5
| Уравнение линии тренда  . .
3. Расчет ошибок.
Ошибки прогнозируемых объемов продаж можно рассчитывать по формуле  . .
Таблица 4
| Номер
квартала
| Объем продаж A,
тыс. шт.
| Сезонная
компонента S
| Десезонализи-рованный объем продаж A / S = T ´ S, тыс. шт.
| Тренд T, тыс. шт.
| Ошибка
E
| |
|
|
|
|
|
| |
|
| 0, 757
| 83, 2
| 82, 8
| 0, 76
| |
|
| 0, 881
| 84, 0
|
| 0, 88
| |
|
| 0, 952
| 83, 0
| 85, 2
| 0, 95
| |
|
| 1, 410
| 85, 1
| 86, 4
| 1, 41
| |
|
| 0, 757
| 88, 5
| 87, 6
| 0, 76
| |
|
| 0, 881
| 89, 7
| 88, 8
| 0, 88
| |
|
| 0, 952
| 92, 4
|
| 0, 95
| |
|
| 1, 410
| 92, 2
| 91, 2
| 1, 41
| |
|
| 0, 757
| 91, 1
| 92, 4
| 0, 76
| |
|
| 0, 881
| 93, 1
| 93, 6
| 0, 88
| |
|
| 0, 952
| 94, 5
| 94, 8
| 0, 95
| 4. Прогнозирование по мультипликативной модели.
MAD» 1, MSE» 1, 6. Ошибки малы, что позволяет получить хорошие краткосрочные прогнозы.
Прогнозные значения определяются по формуле
 . .
Например, прогнозы объемов продаж в 12 и 13 кварталах:
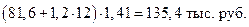 , , 
Литература
1. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2005. – 576 с.
2. Практикум по эконометрике: Учебн. пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.
3. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002. – 311 с.

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Реформы П.А.Столыпина Сегодня уже никто не сомневается в том, что экономическая политика П...
Виды нарушений опорно-двигательного аппарата у детей В общеупотребительном значении нарушение опорно-двигательного аппарата (ОДА) идентифицируется с нарушениями двигательных функций и определенными органическими поражениями (дефектами)...
Особенности массовой коммуникации Развитие средств связи и информации привело к возникновению явления массовой коммуникации...
|
Типовые ситуационные задачи. Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической
Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической нагрузке. Из медицинской книжки установлено, что он страдает врожденным пороком сердца....
Типовые ситуационные задачи. Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт. ст. Влияние психоэмоциональных факторов отсутствует. Колебаний АД практически нет. Головной боли нет. Нормализовать...
Эндоскопическая диагностика язвенной болезни желудка, гастрита, опухоли Хронический гастрит - понятие клинико-анатомическое, характеризующееся определенными патоморфологическими изменениями слизистой оболочки желудка - неспецифическим воспалительным процессом...
|
|


 .
. .
. не равна 4, то их корректируют, путем умножения соответствующей доли на
не равна 4, то их корректируют, путем умножения соответствующей доли на 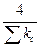 .
. .
. .
. .
. .
.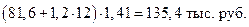 ,
, 



