Построение показательной функции
Уравнение показательной кривой:  . .
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
 . .
Обозначим 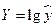 , ,  , ,  . .
Получим линейное уравнение регрессии:
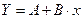 . .
Рассчитаем его параметры, используя данные таблицы 3.
 , ,
 . .
Уравнение будет иметь вид:  . .
Перейдем к исходным переменным x и y, выполнив потенциирование данного уравнения:
 . .
Определим индекс корреляции
 . .
Таблица 3.
|
| y
| Y
| x
| Y× x
| x 2
| 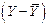
| 
| 
| 
| 
| 
| 
| 
| |
|
| 1, 8062
|
| 115, 60
|
| 0, 1072
| 0, 0115
| ‑ 17, 43
| 303, 76
| 60, 6
| 11, 464
| 3, 3859
| 5, 290
| |
|
| 1, 7482
|
| 118, 88
|
| 0, 0492
| 0, 0024
| ‑ 13, 43
| 180, 33
|
| 3, 9632
| ‑ 1, 991
| 3, 555
| |
|
| 1, 7160
|
| 140, 71
|
| 0, 0170
| 0, 0003
| 0, 57
| 0, 33
| 49, 7
| 5, 4221
| 2, 3285
| 4, 478
| |
|
| 1, 6812
|
| 127, 77
|
| ‑ 0, 017
| 0, 0003
| ‑ 5, 43
| 29, 47
| 53, 1
| 25, 804
| ‑ 5, 08
| 10, 583
| |
|
| 1, 6990
|
| 142, 71
|
| 0, 0000
| 0, 0000
| 2, 57
| 6, 61
| 48, 6
| 2, 0031
| 1, 4153
| 2, 831
| |
|
| 1, 6628
|
| 159, 62
|
| ‑ 0, 036
| 0, 0013
| 14, 57
| 212, 33
| 42, 5
| 11, 933
| 3, 4544
| 7, 509
| |
|
| 1, 5798
|
| 157, 98
|
| ‑ 0, 119
| 0, 0142
| 18, 57
| 344, 90
| 40, 7
| 7, 3132
| ‑ 2, 704
| 7, 117
| | Итого
|
| 11, 8931
|
| 963, 28
|
|
| 0, 0300
|
| 1077, 7
|
| 67, 903
| 0, 8093
| 41, 363
| | Средн. знач.
| 50, 57
| 1, 6990
| 81, 4
| 137, 61
|
|
|
|
|
|
|
|
| 5, 909
| Связь между показателем y и фактором x можно считать достаточно сильной.
Индекс детерминации:
 . .
Вариация результата y (объема выпуска продукции) на 82, 8% объясняется вариацией фактора x (объемом капиталовложений).
Рассчитаем F -критерий Фишера:
 . .
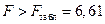 для a = 0, 05; для a = 0, 05;  , ,  . .
Уравнение регрессии с вероятностью 0, 95 в целом статистически значимое, т. к.  . .
Средняя относительная ошибка:
 . .
В среднем расчетные значения  для показательной функции отличаются от фактических на 5.909%. для показательной функции отличаются от фактических на 5.909%.

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...
Интуитивное мышление Мышление — это психический процесс, обеспечивающий познание сущности предметов и явлений и самого субъекта...
Объект, субъект, предмет, цели и задачи управления персоналом Социальная система организации делится на две основные подсистемы: управляющую и управляемую...
|
Реформы П.А.Столыпина Сегодня уже никто не сомневается в том, что экономическая политика П...
Виды нарушений опорно-двигательного аппарата у детей В общеупотребительном значении нарушение опорно-двигательного аппарата (ОДА) идентифицируется с нарушениями двигательных функций и определенными органическими поражениями (дефектами)...
Особенности массовой коммуникации Развитие средств связи и информации привело к возникновению явления массовой коммуникации...
|
|

 .
. .
.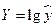 ,
,  ,
,  .
.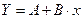 .
. ,
, .
. .
. .
. .
.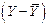







 .
. .
.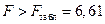 для a = 0, 05;
для a = 0, 05;  ,
,  .
. .
. .
.


