Введение. Важнейшим свойством и признаком полупроводников является зависимость их электрических свойств от внешних условий: температуры
Важнейшим свойством и признаком полупроводников является зависимость их электрических свойств от внешних условий: температуры, освещенности, давления, внешних полей. Формальным, но не решающим признаком принадлежности вещества к классу полупроводников является величина электропроводности σ, которая для них может принимать значение в пределах от 106 – 10-8 Ом-1м-1. К металлам относятся вещества с удельной проводимостью σ = 108 – 107 Ом-1м-1, к диэлектрикам - вещества с σ < 10-12 Ом-1м-1. К классу полупроводников относятся: 1) чистые элементы – B, C, Si, P, S, Ge, As, Sn, Sb, Te, I; 2) большинство минералов, 3) соединения типа АIIBVI (ZnS, CdS, ZnO, …); 3) соединения типа AIIIBV (AlP, AlB, GaP, InSb, GaAs, …); другие соединения и многие органические вещества. Сопротивление металлов при повышении температуры возрастает. Соответствующая зависимость в ограниченном интервале температур может быть представлена линейной функцией:
ρ = ρ 0(1+ α t). (1)
Здесь ρ 0 – удельное сопротивление металлического проводника при t= 0 оС, α – температурный коэффициент сопротивления, различный для разных металлов. Сопротивление полупроводников с ростом температуры падает. Опыт дает зависимость удельного сопротивления от температуры в виде
где T – абсолютная температура образца, а β - параметр, зависящий от механизма проводимости полупроводника и вида примеси, введенной в полупроводник с целью изменения его электрофизических свойств. В некоторой области температур сопротивление полупроводника может возрастать с ростом температуры. Различают собственную и примесную электропроводность полупроводников. Рассмотрим механизм собственной проводимости на примере элемента четвертой группы - германия (или кремния). Атомы германия четырехвалентны. Они образуют кубическую решетку, в которой каждый атом связан парноэлектронной связью с четырьмя ближайшими атомами (один электрон принадлежит данному атому, другой – его соседу). На рис. 1, а связь атомов германия дана на плоской диаграмме. Из рисунка следует, что все электроны связаны со своими атомами. При этом необходимо иметь в виду, что каждый электрон может переходить от атома к атому при встречном движении другого электрона – атомы могут обмениваться электронами. Однако эти электроны не переносят ток – средний заряд, переносимый ими, равен нулю. Прикладываемое внешнее электрическое поле не может вызвать электрического тока, поскольку обычные поля не могут порвать связь электронов с атомами. Для этого требуются поля, сравнимые с внутриатомными.
а) б) Рис. 1
Чтобы электрон стал свободным, необходимо затратить некоторую энергию для разрыва его связи с определенным атомом. Такой энергией может явиться энергия тепловых колебаний решетки, энергия фотона или другого корпускулярного излучения. Освобождение электронов приводит к возникновению электронного механизма переноса тока. Но в собственном полупроводнике появляется и другой механизм. При переходе электрона в свободное состояние вблизи соответствующего атома образуется вакансия – незавершенная ковалентная связь («дырка»). При этом атом имеет избыточный положительный заряд, равный по модулю заряду электрона (рис 1, б). В отсутствии внешнего электрического поля дырки хаотично блуждают по кристаллу. Под воздействием поля, благодаря движению валентных электронов против направления поля, дырки преимущественно перемещается по направлению поля, перенося при этом положительный заряд. Таким образом, в собственном полупроводнике осуществляются электронный (отрицательный) и дырочный (положительный) механизмы переноса тока. При этом концентрация n электронов равна концентрации p дырок. Если подвижности дырок и электронов обозначить через μ pи μ n, то выражение для удельной проводимости собственного полупроводника можно записать в виде
Подвижность электронов и дырок зависит от температуры, однако эта зависимость является слабой. С ростом температуры экспоненциально возрастают концентрации электронов и дырок, что и приводит к экспоненциальной зависимости удельного сопротивления от температуры, выражаемой формулой (2). Рассмотрим далее механизм примесной проводимости полупроводников. Пусть в кристалле германия имеется в виде примеси элемент пятой группы периодической таблицы, например фосфор. Атом его имеет пять валентных электронов. Четыре из них осуществят парноэлектронную связь с ближайшими четырьмя атомами германия. Один из валентных электронов фосфора оказывается незанятым. Он испытывает притяжение со стороны соседних атомов. В результате его энергия связи с атомом фосфора уменьшается приблизительно в ε 2 раз, где ε – диэлектрическая проницаемость германия, равная 16. Поэтому достаточно незначительной энергии, чтобы оторвать этот электрон от атома фосфора; при этом атом фосфора приобретает избыточный положительный заряд, становится ионом, но вакансия (дырка) в ковалентной связи не образуется. При наложении внешнего электрического поля ток будет осуществляться только электронами. Рассматриваемая примесь (она называется донорной) обусловливает электронный механизм проводимости полупроводника. Изменяя концентрацию примесных атомов, можно в широких пределах изменять электрофизические свойства полупроводника. В электронном полупроводнике возможно наличие некоторого количества дырок, возникающих при ионизации атомов самого германия. Но так как для этого требуется значительно большая энергия, то концентрация дырок будет значительно меньше концентрации электронов до тех пор, пока в полупроводнике имеются неионизованные примесные атомы. Дырки в электронном полупроводнике называются неосновными носителями тока. Возможно осуществление другого механизма электропроводности полупроводника. Действительно, пусть в германий введен в качестве примеси элемент третьей группы, например бор (акцепторная примесь). Он имеет три валентных электрона, которые могут осуществить связь с тремя атомами германия. Одна связь оказывается незавершенной. Для ее завершения атом бора должен захватить электрон, принадлежащий атомам германия. Для такого перехода электрон должен получить дополнительную энергию, которая гораздо меньше энергии, необходимой для возбуждения пары электрон-дырка. Такой энергией может явиться энергия тепловых колебаний или энергия кванта света. При переходе электрона на примесный атом этот атом становится отрицательно заряженным ионом, а незавершенная связь у пары атомов германия будет блуждать по кристаллу. При наложении внешнего поля дырка будет двигаться, дрейфовать по полю, отрицательный же заряд связан с атомом бора и принимать участия в переносе тока не будет. Следовательно, в акцепторном полупроводнике носителями тока будут дырки. Количество неосновных носителей – электронов – при не очень высоких температурах будет значительно меньше, чем число дырок. Теоретический расчет методами статистической физики дает экспоненциальную зависимость концентрации свободных электронов и дырок от температуры T. При этом в области в области собственной проводимости
где параметр Δ E соответствует энергии, необходимой для образования пары электрон-дырка в кристалле, k – постоянная Больцмана. В области примесной проводимости зависимость концентрации электронов или дырок также дается формулой (4), при этом параметр Δ E соответствует энергии, необходимой для ионизации атома донорной примеси или энергии, необходимой для перевода электрона от основного атома кристалла на атом акцепторной примеси. В соответствии с (3) аналогичная зависимость имеет место для удельной электропроводности полупроводника. Следовательно, сопротивление полупроводникового образца будет экспоненциально уменьшаться с ростом температуры:
Здесь параметр A соответствует сопротивлению образца при температуре Логарифмируя выражение (5), мы получим:
Экспоненциальную зависимость сопротивления от температуры легко выявить, если по результатам эксперимента построить график зависимости ln R от 1/ T: экспериментальные точки в таких координатах должны укладываться на прямую линию. Более того, по наклону графика можно определить параметр Δ E. Приведем табличные значения параметра Δ E для кремния и германия. · Для собственной (электронно-дырочной) проводимости: Δ E (Si) = 1, 1эВ; Δ E (Ge) = 0, 72 эВ. · Для электронной проводимости, обусловленной примесью фосфора: Δ E (Si) = 0, 044эВ; Δ E (Ge) = 0, 012 эВ. · Для дырочной проводимости, обусловленной примесью бора: Δ E (Si) = 0, 045эВ; Δ E (Ge) = 0, 012 эВ. Таким образом, энергия ионизации примесного атома существенно меньше энергии, необходимой для образования пары «электрон-дырка» как в кремнии, так и в германии. При контакте двух разнородных полупроводников – с электронной и дырочной проводимостью – в области контакта вследствие диффузии и рекомбинации электронов и дырок возникает двойной электрический слой, в котором отсутствуют основные носители тока (см. Введение к лаб. работе №). Этот слой (p-n- переход) обладает свойством односторонней проводимости, которое находит широкие технические применения в полупроводниковой электронике и электротехнике. С ила обратного тока, текущего через p-n-переход, уже при малых значениях напряжения испытывает насыщение и определяется концентрацией неосновных носителей, возникающих вследствие ионизации атомов германия (кремния) тепловыми колебаниями. Таким образом, исследуя зависимость от температуры силы обратного тока, текущего через p-n-переход, можно найти значение важнейшего параметра полупроводника – энергии Δ E, необходимой для образования пары электрон-дырка в кристалле.
|

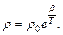 (2)
(2)
 (3)
(3) (4)
(4) (5)
(5)
 . (6)
. (6)


