Министерство здравоохранения и социального развития РФ
5.1.Поток векторного поля
Пусть каждой точке М(x, y, z) некоторой области пространства соответствует вектор а (М). В этом случае говорят, что в этой области пространства задано векторное поле (или вектор-функция точки). Поверхностный интеграл I рода по поверхности S от скалярного произведения вектора поля на единичный вектор нормали к поверхности называют потоком поля через поверхность. Таким образом, поток К векторного поля а через поверхность S вычисляется по формуле: К = Пример. Найдем поток векторного поля a = z i – x j + y k через верхнюю сторону треугольника, полученного при пересечении плоскости 3 х +6 у –2 z –6=0 с координатными плоскостями. К = Для данной плоскости орт нормали n = ±( К = Итак, К =
5.2. Дивергенция векторного поля
Пусть каждой точке М(x, y, z) некоторой области пространства соответствует вектор а (М)={P(x, y, z); Q(x, y, z); R(x, y, z)}. Дивергенцией такого векторного поля в точке М называется число div a (M) = Используя понятие дивергенции, можно переписать формулу Остроградского-Гаусса в векторной форме:
5.3. Циркуляция векторного поля
Пусть каждой точке М(x, y, z) некоторой области пространства соответствует вектор а (М)={P(x, y, z); Q(x, y, z); R(x, y, z)}. Выберем в этой области гладкую замкнутую кривую L. Циркуляцией векторного поля вдоль контура L называется число C= Пример. Вычислим циркуляцию векторного поля a =(x –2 z) i +(x +3 y + z) j +(5 x + y) k вдоль контура треугольника с вершинами А(1; 0; 1), В(0; 1; 0) и С(0; 0; 1). C=
На отрезке АВ х + у =1, z =0, поэтому
5.4. Ротор векторного поля
Пусть каждой точке М(x, y, z) некоторой области пространства соответствует вектор а (М)={P(x, y, z); Q(x, y, z); R(x, y, z)}. Ротором векторного поля в точке М называется вектор rot a (M) = rot a (M) = Используя понятия циркуляции и ротора, можно переписать формулу Стокса в векторной форме:
СПИСОК ЛИТЕРАТУРЫ
Св. план г., поз.
Арутюнян Елена Бабкеновна
Математика Часть 3
Учебное пособие
___________________________________________
Подписано в печать Тираж – 100 экз. Усл.-печ. л. – Формат Заказ _____________________________________________________________
127994, Москва, ул. Образцова, д.9, стр.9. Типография МИИТа Министерство здравоохранения и социального развития РФ ГОУВПО «Ставропольская государственная медицинская академия»
|

 . Заметим, что подынтегральная функция равна проекции вектора поля на единичный вектор нормали к поверхности. Используя связь поверхностных интегралов I и II рода, поток можно записать в виде: К =
. Заметим, что подынтегральная функция равна проекции вектора поля на единичный вектор нормали к поверхности. Используя связь поверхностных интегралов I и II рода, поток можно записать в виде: К =  , где P, Q, R – проекции вектора поля на координатные оси.
, где P, Q, R – проекции вектора поля на координатные оси.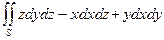 .
. ;
;  ; –
; –  ). Так как на верхней стороне плоскости он образует с осью O z острый угол, то выбираем n = (–
). Так как на верхней стороне плоскости он образует с осью O z острый угол, то выбираем n = (–  , где области интегрирования – проекции треугольника на соответствующие координатные плоскости.
, где области интегрирования – проекции треугольника на соответствующие координатные плоскости.  ;
;  ;
; 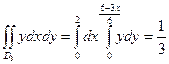 .
. + 2 +
+ 2 +  =
=  .·
.·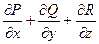 .
. =
= 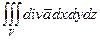 , – поток векторного поля через замкнутую поверхность в направлении «изнутри» равен интегралу дивергенции этого поля по объему, ограниченному данной поверхностью.
, – поток векторного поля через замкнутую поверхность в направлении «изнутри» равен интегралу дивергенции этого поля по объему, ограниченному данной поверхностью. .
. =
=  +
+  +
+  .
. . Аналогично
. Аналогично  . Удобно записывать ротор в виде определителя:
. Удобно записывать ротор в виде определителя: .
. =
= 


