Коэффициент вариации
Величина среднего квадратического отклонения обычно характеризует степень рассеянности ряда при сравнении однотипных рядов. Если сравниваются два ряда с разными признаками (рост и вес, средняя длительность лечения на дому и частота врачебных посещений), то такое составление сигм невозможно. В этих случаях применяют коэффициент вариации, представляющей собой степень рассеянности ряда в относительных величинах. Формула его вычисления:
d – среднее квадратическое отклонение; M – средняя арифметическая Чем выше коэффициент вариации, тем больше изменчивость данного признака. Считают, что Со > 30% говорит о качественной неоднородности совокупности. Кроме М; d и Со в ряде случаев используются еще два обобщающих коэффициента — Мо (мода) и Me (медиана). Мода — это наиболее часто встречающаяся варианта в изучаемом вариационном ряду. Она часто используется при обработке небольших выборок, когда гетерогенный состав совокупности обеспечивает смысл средней арифметической. Медиана — варианта, которая делит вариационный ряд на две равные части. С помощью медианы в таблицах смертности определяется вероятная продолжительность предстоящей жизни, вычисляется средний радиус обслуживания лечебно-профилактического учреждения и т. п. Для определения степени достоверности результатов статистического исследования нужно для каждого относительно небольшого показателя и для каждой средней величины вычислять так называемые средние ошибки этих величин. Вычисление средней ошибки (t) для относительных величин производится по формуле:
Для средней арифметической средняя ошибка равна:
Величина средней ошибки показывает, в каких пределах может колебаться размер статистического показателя или средней величины в зависимости от влияния причин, которые не могут быть учтены в данном случае (случайные причины). Таким образом, определяют так называемые доверительные границы относительного показателя или средней величины. Доверительные границы определяются по формуле: P±tm для относительных величин и M±tm для средних величин. В этих формулах Р обозначает величину относительного показателя; М — размеры средней арифметической; t берется в соответствии с изложенными выше указаниями; m исчисляется по приведенным ранее формулам. Так, например, на основании измерения веса определенного правильно отобранного количества детей данного поселка установлено, что М величина веса восьмилетних мальчиков равна 23, 89 кг, а средняя ошибка этой величины 0, 14 кг. Контрольные вопросы: 1) Дайте определение вариационного ряда. 2) Виды вариационных рядов. 3) Каковы виды средних и порядок их вычисления? 4) Что такое d? 5) Какие способы и порядок вычисления d вы знаете? 6) Какой коэффициент характеризует степень рассеянности ряда? Формула его вычисления. 7) Что представляет из себя амплитуда колебания? 8) Степень вариации, ее характеристика. Формула для ее вычисления. 9) От чего зависит величина ошибки средней (t)? 10) Как вы понимаете термин “доверительные границы”? 11) Методика определения доверительных границ относительного показателя. 12) Методика определения доверительных границ средней величины.
|

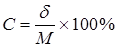 , где
, где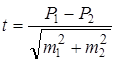
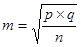 , где р – величина показателя.
, где р – величина показателя.


