Тема № 4. Оценка достоверности результатов исследования
Цель занятия: изучить понятие достоверности результатов исследования, его оценки, уметь определять ошибки относительных величин, достоверность разности между двумя относительными или средними величинами, критерии безошибочного прогноза. Основные теоретические положения темы: при вычислении показателей часто используют не всю генеральную совокупность, а только какую-то ее часть. Для того, чтобы по части явления можно было судить о явлении в целом, о его закономерностях, необходима оценка достоверности результатов исследования. Мерой достоверности показателя является его ошибка, показывающая, насколько результат, полученный при выборочном исследовании, отличается от результата, который мог бы быть получен при сплошном исследовании всей генеральной совокупности. Средняя ошибка относительных величин определяется по формуле:
При числе наблюдений менее 30 в формулу вводится поправка:
p – величина показателя; q = 100 – p Установлено:
При медицинских и биологических исследованиях считается достаточным, если критерий достоверности t ³ 2. Достоверность разности между двумя относительными величинами определяется по формуле: Полученный критерий оценивается по общепринятым правилам. При сопоставлении средних величин t рассчитывается по формуле: Оценка t производится так же, как и при расчете относительных величин. Контрольные вопросы: 1) Какова формула вычисления ошибки средней (t) для коэффициентов? 2) От чего зависит величина ошибки средней (t)? 3) Какова формула средней ошибки разности показателей? 4) В каком случае разность средних и показателей считается существенной? 5) Можно ли по величине критерия судить о степени различия между ожидаемыми и фактическими числами? 6) Что нужно знать, чтобы ответить на вопрос, достоверно или нет отличие фактических и ожидаемых чисел?
|




 , где
, где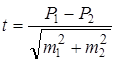 , где: Р1 и Р2 – показатели, полученные при выборочных исследованиях; m1 и m2 – соответствующие ошибки.
, где: Р1 и Р2 – показатели, полученные при выборочных исследованиях; m1 и m2 – соответствующие ошибки. , где: М1 и М2 – сравниваемые величины, а m1 и m2 – их ошибки.
, где: М1 и М2 – сравниваемые величины, а m1 и m2 – их ошибки.


