Тема № 5. Методы корреляционного анализа
Цель занятия: изучить виды проявления корреляционных связей между явлениями, понятие функциональной и корреляционной зависимости, практическое значение установление корреляционной связи, характеристику коэффициента корреляции по силе и направлению, методику и порядок вычисления коэффициента корреляции методом рангов, ошибок коэффициента корреляции и способы оценки достоверности коэффициента корреляции. Основные теоретические положения темы: При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой-либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции. Все явления в природе и в обществе находятся во взаимной связи. Различают две формы проявления количественных связей между признаками: функциональную и корреляционную. Функциональная связь — такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-химических процессов. Корреляционная связь — такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для социально-гигиенических процессов, клинической медицины и биологии. Практическое значение установления корреляционной связи: 1. Выявление причинно-следственной связи между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.). 2. Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др. Корреляционный анализ позволяет изучить взаимодействие факторов, измерить “силу” характер и направленность влияния одних факторов на другие. Величиной, характеризующей направление и силу связи между признаками, является коэффициент корреляции. Корреляционная связь может быть представлена таблицей, графиком (диаграмма рассеяния) или коэффициентом корреляции. Измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту). Расчет может производиться с использованием как абсолютных, так и производных величин. Для вычисления коэффициента корреляции используются несгруппированные данные (это требование применяется только при вычислении коэффициента корреляции по методу квадратов). Число наблюдений не менее 30. Коэффициент корреляции одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ±1.
По характеру зависимость между факторами может быть линейной, когда при изучении одного фактора другой также пропорционально меняется и криволинейной, когда происходят непропорциональные изменения. По направленности влияние одного фактора на другой бывает положительным, когда с увеличением одного фактора, другой также увеличивается, и отрицательным, когда при увеличении одного фактора, другой уменьшается. Метод ранговой корреляции применяется в тех случаях, когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных, когда признаки не только количественные, но и атрибутивные и ряды распределения признаков имеют открытые варианты (например: стаж работы до 1 года). Оценка достоверности коэффициента корреляции определяется в зависимости от метода вычисления коэффициента корреляции:
Ошибка коэффициента корреляции, вычисленного методов квадратов (Пирсона): Ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена): Критерий достоверности определяется по формуле: Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n – 2), где n – число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности P ³ 99%. Контрольные вопросы: 1) Дайте определение функциональной и корреляционной связи. 2) Приведите примеры прямой и обратной корреляционной связи. 3) Укажите размеры коэффициентов корреляции при слабой, средней и сильной связи между признаками. 4) В каких случаях применяется ранговый метод вычисления коэффициента корреляции? 5) Каковы основные этапы вычисления коэффициента корреляции ранговым методом? 6) Как определяется достоверность коэффициента корреляции? Укажите способы.
|



 или
или 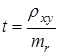 , где rxy – коэффициент корреляции, x и y – признаки, между которыми определяется связь, n – число наблюдений.
, где rxy – коэффициент корреляции, x и y – признаки, между которыми определяется связь, n – число наблюдений.


