Задачи для самостоятельного решения. 1. Прибыль потребителя 10 руб
1. Прибыль потребителя 10 руб. Предельная полезность имеет следующую динамику: 1 часть – 10 руб., 2-я часть – 9 руб., 3-я часть – 7, 5 руб., 4-я часть – 5, 5 руб., 5-я часть – 3 руб. Определите количество купленного товара. Решение: прибыль потребителя есть разница между общей полезностью (TU) и затратами на покупку товара (PQ). При покупке первой части прибыль составит: 10 – 10*1 = 0; 2-ой части: (10+9) – 9*2 = 1; 3-ей части: (10 + 9 + 7, 5) – 7, 5*3 = 4; 4-ой части: (10 + 9 + 7, 5 + 5, 5) – 5, 5*4 = 10. Значит, потребитель купит 4 единицы товара. Ответ: потребитель приобретет 4 единицы товара.
2. Потребитель тратит 2 долл. в день на бананы и яблоки. MU яблок для него равна: 2 – 3х, где х – количество яблок, шт. MU бананов равна: 4 – 5у, где у – количество бананов, шт. Цена одного яблока – 10 центов, цена одного банана – 50 центов. Какое количество яблок и бананов купит рациональный потребитель? Решение: 1) В состояние равновесия отношение предельных полезностей равно отношению цен товаров:
2) Выбор потребителя предопределен бюджетным ограничением: PхХ + PуУ = I 3) Поэтому: Решая систему уравнений, получаем ответ: х = 5, у = 3. Ответ: рациональный потребитель купит 5 яблок и 3 банана.
3.На рисунке показана кривая безразличия потребителя и его бюджетная линия. Напишите уравнение бюджетной линии, если цена товара У равна 6 долл. Варианты ответов: а) QY = 10 – 1, 5QX; б) QY = 15 – 1, 5QX; в) QY = 15 – 0, 67QX; г) QY = 10 – 0, 67QX.
Решение: доход потребителя равен: 10 * 6 = 60, отсюда цена товара Х равна: 60/15 = 4. Тогда уравнение бюджетной линии будет иметь вид: 60 = 4QX + 6QY, откуда следует: 6QY = 60 – 4QX и, соответственно QY = 10 – 0, 67QX. Ответ: г) QY = 10 – 0, 67QX.
|


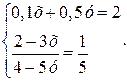
 Товар У
Товар У
 Товар Х
Товар Х


