Линейные уравнения
Определение. Дифференциальное уравнение Общий вид уравнения
где Определение. Если функция Определение. Если функция
Сформулируем некоторые свойства линейных однородных уравнений, ограничиваясь в доказательствах уравнениями второго порядка
Лемма. (Свойство решений линейного однородного уравнения) Решения линейного однородного уравнения (2.11) можно умножать на произвольные постоянные и складывать, после чего опять получается решение уравнения (2.11). Доказательство. Действительно, если Это свойство имеет место для линейного однородного уравнения любого порядка. Заметим, что уравнение (2.11) всегда имеет нулевое решение. В дальнейшем, говоря о решениях уравнения (2.11) будем подразумевать, что эти решения отличны от нулевого. Определение. Два решения уравнения (2.11) называются линейно независимыми на отрезке [a, b], если их отношение не является постоянным на этом отрезке, т.е. Пример. Рассмотрим линейное уравнение Функции
|

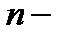 го порядка называется линейным, если оно первой степени относительно искомой функции и ее производных
го порядка называется линейным, если оно первой степени относительно искомой функции и ее производных  /
/ . (2.10)
. (2.10) – заданные функции или постоянные. Функция
– заданные функции или постоянные. Функция  называется правой частью уравнения.
называется правой частью уравнения.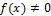 , то уравнение (2.10) называется неоднородным линейным уравнением или уравнением с правой частью.
, то уравнение (2.10) называется неоднородным линейным уравнением или уравнением с правой частью. , то уравнение (2.10) называется однородным линейным уравнением или уравнением без правой части и имеет вид
, то уравнение (2.10) называется однородным линейным уравнением или уравнением без правой части и имеет вид
 (2.11)
(2.11) есть решение уравнения (2.11), т.е.
есть решение уравнения (2.11), т.е.  , то очевидно
, то очевидно  , т.е. и
, т.е. и  также решение уравнения (2.11). Точно так же, если
также решение уравнения (2.11). Точно так же, если  и
и  решения (2.11), то
решения (2.11), то  есть также его решение, причем
есть также его решение, причем  и
и  произвольные постоянные.
произвольные постоянные. . В противном случае решения называются линейно зависимыми.
. В противном случае решения называются линейно зависимыми.
 являются решениями этого уравнения. Это легко проверить подстановкой их в уравнение. Функции.
являются решениями этого уравнения. Это легко проверить подстановкой их в уравнение. Функции.  , а функции
, а функции  линейно зависимы
линейно зависимы 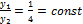 .
.


