Определение. Если  и
и 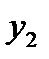 - два решения уравнения (2.11), то выражение, составленное из них
- два решения уравнения (2.11), то выражение, составленное из них
 , (2.12)
, (2.12)
называется определителем Вронского.
В дальнейшем будем рассматривать решения уравнения (2.11) на промежутке  непрерывности коэффициентов
непрерывности коэффициентов  ,
,  .
.
Необходимое и достаточное условие линейной зависимости решений дает
Теорема. Равенство нулю определителя Вронского  является необходимым и достаточным условием линейной зависимости решений
является необходимым и достаточным условием линейной зависимости решений  и
и  , т.е. два решения
, т.е. два решения  и
и  уравнения (2.11) линейно независимы тогда и только тогда, когда определитель Вронского
уравнения (2.11) линейно независимы тогда и только тогда, когда определитель Вронского  отличен от нуля.
отличен от нуля.
Лемма. Если  и
и  - два линейно независимых решения уравнения (2.11), то формула
- два линейно независимых решения уравнения (2.11), то формула
 , (2.11а)
, (2.11а)
где  и
и  - произвольные постоянные, дает все решения этого уравнения.
- произвольные постоянные, дает все решения этого уравнения.
Теорема. Если  - частное решение уравнения (2.11), то второе его решение, линейно независимое с первым, можно найти по формуле
- частное решение уравнения (2.11), то второе его решение, линейно независимое с первым, можно найти по формуле
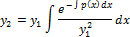
Пример. Записать общее решение уравнения  , если известно его частное решение
, если известно его частное решение  .
.
Решение. В нашем случае  и используя формулу
и используя формулу  получаем:
получаем:
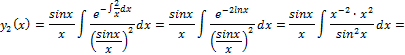
= 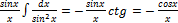
Общее решение:
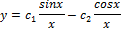
Определение. Определителем Вронского (вронскианом) системы функций  называется определитель
называется определитель
 . (2.13)
. (2.13)
На решения  уравнения (2.10) распространяются определения линейной зависимости (независимости) и теорема о необходимом и достаточном условии линейной зависимости решений.
уравнения (2.10) распространяются определения линейной зависимости (независимости) и теорема о необходимом и достаточном условии линейной зависимости решений.
Пример. Исследовать на линейную зависимость системы функций:
1.  ;
;
2.  .
.
Решение.
1. Составив и вычислив вронскиан по формуле (2.12)
 , получим, что система функций
, получим, что система функций  - линейно независима.
- линейно независима.
2. Составив и вычислив вронскиан по формуле (2.13)
 получим, что система функций
получим, что система функций  - линейно зависима.
- линейно зависима.
Определение. Всякая система из  линейно независимых решений
линейно независимых решений  уравнения (2.10) называется фундаментальной системой решений этого уравнения.
уравнения (2.10) называется фундаментальной системой решений этого уравнения.
Если известна фундаментальная система решений уравнения (2.10), то общее решение этого уравнения имеет вид
 , (2.14)
, (2.14)
где 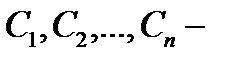 произвольные постоянные.
произвольные постоянные.
Пример. Функции  образуют фундаментальную систему решений уравнения
образуют фундаментальную систему решений уравнения  . Найти общее решение этого уравнения.
. Найти общее решение этого уравнения.
Решение. По формуле (2.14) имеем  , где
, где  произвольные постоянные.
произвольные постоянные.

 и
и 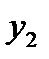 - два решения уравнения (2.11), то выражение, составленное из них
- два решения уравнения (2.11), то выражение, составленное из них , (2.12)
, (2.12) непрерывности коэффициентов
непрерывности коэффициентов  ,
,  .
. является необходимым и достаточным условием линейной зависимости решений
является необходимым и достаточным условием линейной зависимости решений  и
и  , т.е. два решения
, т.е. два решения  и
и  уравнения (2.11) линейно независимы тогда и только тогда, когда определитель Вронского
уравнения (2.11) линейно независимы тогда и только тогда, когда определитель Вронского  отличен от нуля.
отличен от нуля. и
и  - два линейно независимых решения уравнения (2.11), то формула
- два линейно независимых решения уравнения (2.11), то формула , (2.11а)
, (2.11а) и
и  - произвольные постоянные, дает все решения этого уравнения.
- произвольные постоянные, дает все решения этого уравнения. - частное решение уравнения (2.11), то второе его решение, линейно независимое с первым, можно найти по формуле
- частное решение уравнения (2.11), то второе его решение, линейно независимое с первым, можно найти по формуле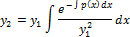
 , если известно его частное решение
, если известно его частное решение  .
. и используя формулу
и используя формулу  получаем:
получаем: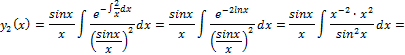
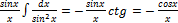
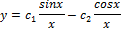
 называется определитель
называется определитель . (2.13)
. (2.13) уравнения (2.10) распространяются определения линейной зависимости (независимости) и теорема о необходимом и достаточном условии линейной зависимости решений.
уравнения (2.10) распространяются определения линейной зависимости (независимости) и теорема о необходимом и достаточном условии линейной зависимости решений. ;
; .
. , получим, что система функций
, получим, что система функций  - линейно независима.
- линейно независима. получим, что система функций
получим, что система функций  - линейно зависима.
- линейно зависима. линейно независимых решений
линейно независимых решений  уравнения (2.10) называется фундаментальной системой решений этого уравнения.
уравнения (2.10) называется фундаментальной системой решений этого уравнения. , (2.14)
, (2.14) произвольные постоянные.
произвольные постоянные. образуют фундаментальную систему решений уравнения
образуют фундаментальную систему решений уравнения  . Найти общее решение этого уравнения.
. Найти общее решение этого уравнения. , где
, где  произвольные постоянные.
произвольные постоянные.


