Коэффициентами. Общий вид линейного дифференциального уравнения порядка с постоянными коэффициентами есть
Общий вид линейного дифференциального уравнения порядка
где Определение. Уравнение
полученное заменой производных Каждому действительному корню
а каждой паре комплексных корней
Запишем общее решение для случая
где Характеристическое уравнение для (2.22) имеет вид
Если квадратное уравнение (2.23) имеет два различных действительных корня
Общее решение имеет вид
где Если квадратное уравнение (2.23) имеет комплексные корни
Общее решение имеет вид
Если квадратное уравнение (2.23) имеет два равных действительных корня
Общее решение уравнения имеет вид
Примеры. Найти общее решение уравнений:
1 2 3
|
с постоянными коэффициентами есть
, (2.18)
- действительные постоянные.
, (2.19)
искомой функции степенями 
, называется характеристическим уравнением для уравнения (2.18).
уравнения (2.19) кратности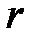 
соответствуют 
, (2.20)
кратности 
соответствуют 
пар линейно независимых решений:
(2.21)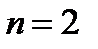
. Рассмотрим уравнение
, (2.22)
- действительные числа.
. (2.23)
и 
, то согласно (2.20) имеем два линейно независимых решения уравнения (2.22)
.
, (2.24)
- произвольные постоянные.
, тогда согласно (2.21) имеем два линейно независимых решения уравнения (2.22)
.
. (2.25)
, то согласно (2.20) имеем два линейно независимых решения уравнения (2.22)
.
. (2.26)
;
;
.
