Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами
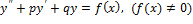 , (2.14)
, (2.14)
где  действительные числа.
действительные числа.
Общее решение этого уравнения записывается в виде  , где
, где  - общее решение соответствующего однородного уравнения (2.11),
- общее решение соответствующего однородного уравнения (2.11),  любое частное решение уравнения (2.14). Общее решение ОДУ (2.10)
любое частное решение уравнения (2.14). Общее решение ОДУ (2.10)  , для отыскания
, для отыскания  в общем случае используется метод Лагранжа вариации произвольных постоянных, рассмотренный в пункте 2.3.3.
в общем случае используется метод Лагранжа вариации произвольных постоянных, рассмотренный в пункте 2.3.3.
Пример. Найти общее решение уравнения
 .
.
1. Решим однородное уравнение  . Для чего запишем характеристическое уравнение
. Для чего запишем характеристическое уравнение

 . Согласно (2.19), (2.20) фундаментальная система решений будет иметь вид
. Согласно (2.19), (2.20) фундаментальная система решений будет иметь вид 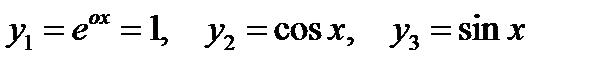 , следовательно, общее решение однородного уравнения
, следовательно, общее решение однородного уравнения
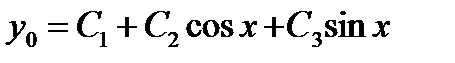 .
.
Для нахождения частного решения неоднородного уравнения воспользуемся методом вариации произвольных постоянных. Ищем частное решение в виде
 . Для определения
. Для определения 
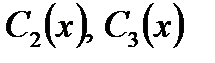 составим систему
составим систему
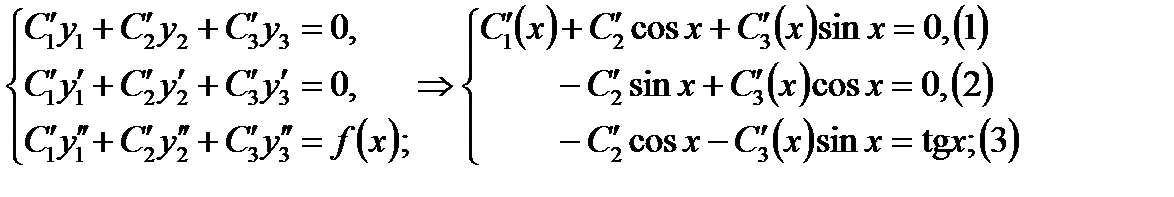
Умножив обе части второго уравнения на  , третьего - на
, третьего - на  и сложив, получим
и сложив, получим
 .
.
Подставив  в уравнение (2), получим
в уравнение (2), получим
 .
.
Сложив уравнения (1) и (3) будем иметь  .
.
Интегрирование дает выражения для 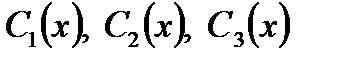 :
:


Итак, 
Учитывая, что 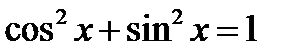 , получим искомое решение неоднородного уравнения
, получим искомое решение неоднородного уравнения
 , где
, где 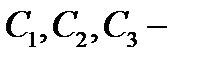 произвольные постоянные.
произвольные постоянные.

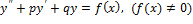 , (2.14)
, (2.14) действительные числа.
действительные числа. , где
, где  - общее решение соответствующего однородного уравнения (2.11),
- общее решение соответствующего однородного уравнения (2.11),  любое частное решение уравнения (2.14). Общее решение ОДУ (2.10)
любое частное решение уравнения (2.14). Общее решение ОДУ (2.10)  , для отыскания
, для отыскания  в общем случае используется метод Лагранжа вариации произвольных постоянных, рассмотренный в пункте 2.3.3.
в общем случае используется метод Лагранжа вариации произвольных постоянных, рассмотренный в пункте 2.3.3. .
. . Для чего запишем характеристическое уравнение
. Для чего запишем характеристическое уравнение
 . Согласно (2.19), (2.20) фундаментальная система решений будет иметь вид
. Согласно (2.19), (2.20) фундаментальная система решений будет иметь вид 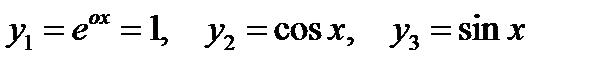 , следовательно, общее решение однородного уравнения
, следовательно, общее решение однородного уравнения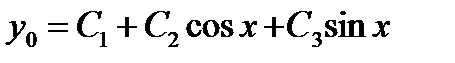 .
. . Для определения
. Для определения 
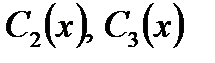 составим систему
составим систему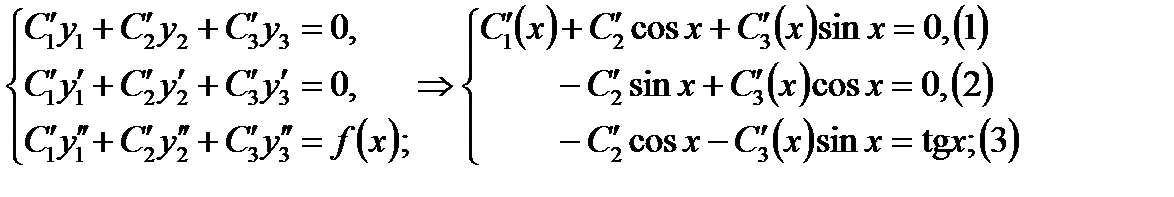
 , третьего - на
, третьего - на  и сложив, получим
и сложив, получим .
. в уравнение (2), получим
в уравнение (2), получим .
. .
.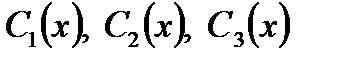 :
:


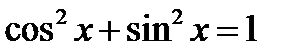 , получим искомое решение неоднородного уравнения
, получим искомое решение неоднородного уравнения , где
, где 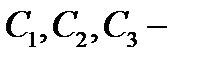 произвольные постоянные.
произвольные постоянные.


