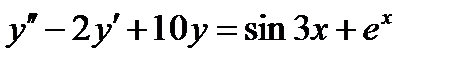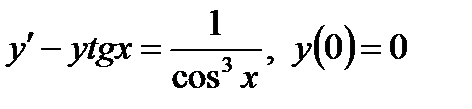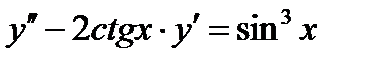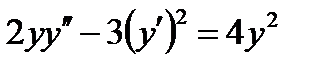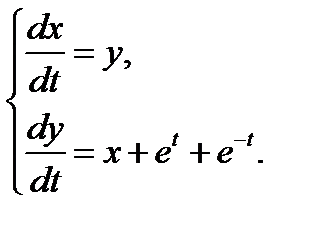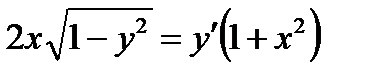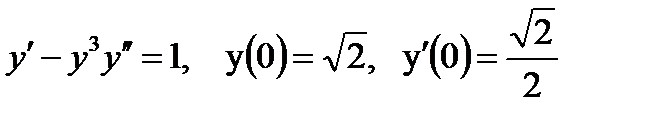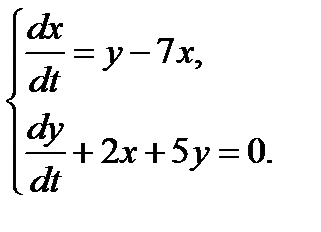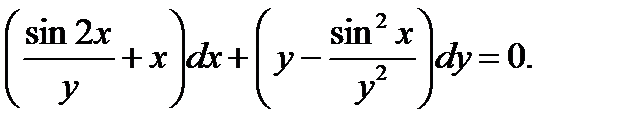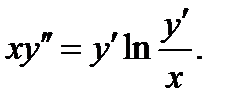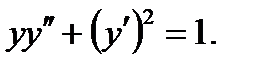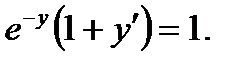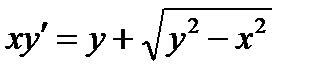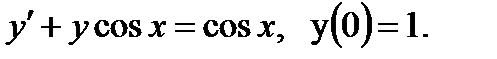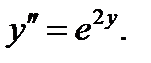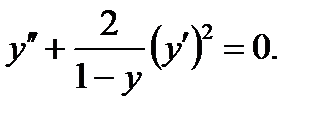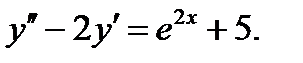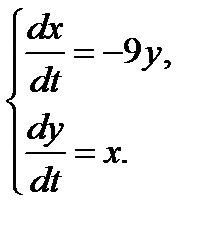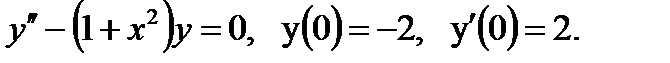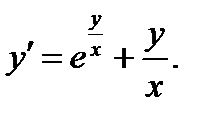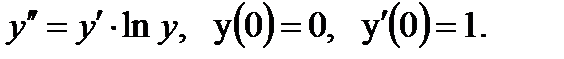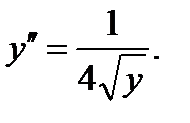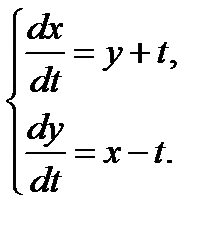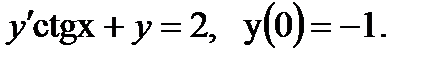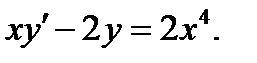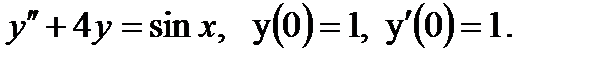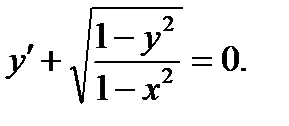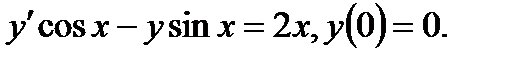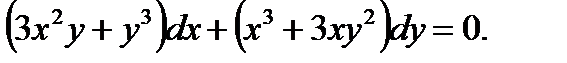Основные правила и требования
Каждый студент выполняет один вариант задания. Выбор варианта осуществляется по номеру в журнале группы или по указанию преподавателя. Преподаватель также определяет, какие задачи должен решить каждый студент. Сроки выполнения и сдачи студентами расчетно-графической работы устанавливаются и контролируются преподавателем в соответствии с рабочей программой по дисциплине. Предварительно проверяется правильность решения задач. Завершающим этапом является защита задания. Во время защиты студент должен уметь правильно отвечать на теоретические вопросы, пояснять решения упражнений и задач, решать задачи аналогичного типа. В каждый вариант включены основные типы дифференциальных уравнений: первого порядка с разделяющимися переменными; однородные уравнения; линейные и уравнения Бернулли; уравнения в полных дифференциалах; уравнения
Примерный типовой вариант №0
Решить: 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.10 0.11 0.12 0.13
0.14 Найти кривую, проходящую через точку (3; 2), для которой отрезок любой её касательной, заключённой между координатными осями, делится пополам в точке касания. 0.15 В 1980 году в городе проживало 100000 жителей. В течение последующих лет население города увеличивалось со скоростью, пропорциональной числу жителей в текущий момент времени. В 1990 году в городе проживало 120000 жителей. Сколько жителей должно проживать в 2000 году?
Решение примеров типового варианта №0 Пример 0.1 Решение: Разделим переменные:
Проинтегрируем обе части последнего равенства
По свойству логарифмов
Пример 0.2
Решение: Данное дифференциальное уравнение относится к типу однородных дифференциальных уравнений Производя обратную замену Используя начальное условие Итак, искомое решение имеет вид: y=2x arctgx
Пример 0.3 Решение: Данное уравнение относится к типу линейных дифференциальных уравнений первого порядка а. Решение методом Лагранжа – метод вариации произвольной постоянной. Первоначально решим однородное уравнение, заменив правую часть нулем:
Это уравнение с разделяющимися переменными:
Интегрируем последнее уравнение и находим
Ищем решение исходного неоднородного уравнения в виде
После очевидных сокращений, будем иметь
Таким образом, получаем общее решение исходного уравнения:
б. Решение методом Бернулли — подстановка Подставим в исходное уравнение
или
Полагаем, что Полученные значения и и v подставляем в формулу у=uv и окончательно находим общее решение исходного дифференциального уравнения в виде
который естественно совпадает с ответом, найденным по методу Лагранжа.
Пример 0.4 Решение: Проверим, не является ли это уравнение дифференциальным уравнением в полных дифференциалах. Если
Поскольку Из первого уравнения находим:
Продифференцируем полученный результат по у и подставим во второе уравнение:
После элементарных преобразований получим
После подстановки найденного значения
Пример 0.5 Решениие: Это дифференциальное уравнение второго порядка типа Интегрируя последнее уравнение, находим
решая которое методом интегрирования по частям найдем ответ:
Пример 0.6 Решение: Введем переменную
Воспользовавшись начальными условиями, найдем:
Следовательно, искомое частное решение имеет вид
Пример 0.7 Р е ш е н и е: Это дифференциальное уравнение второго порядка типа Так как Интегрируя, получаем общий интеграл
Отсюда находим общее решение:
Пример 0.8 Решение: Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение данного дифференциального уравнения имеет вид
Пример 0.9 Решение: Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общее решение этого уравнения можно записать в виде суммы Находим его корни Правая часть исходного уравнения
Находим
Подставляя выражения
После приведения подобных членов находим
Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений
из которой находим Подставляя найденные значения А и В в выражение для
Общее решение исходного уравнения будет иметь вид:
Пример 0.10 Решение: Это линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, по типу и методу решения аналогичное уравнению рассмотренному в примере 0.9. Составим характеристическое уравнение для однородного уравнения
Правая часть исходного уравнения имеет вид
где r равно числу корней характеристического уравнения совпадающих с bi. В нашем примере
Находим
Приравнивая коэффициенты при одинаковых тригонометрических функциях, будем иметь:
Таким образом
Пример 0.11 Решение: Это линейное неоднородное дифференциальное уравнение второго порядка с переменными коэффициентами. Для его решения используем метод вариации произвольных постоянных. Прежде всего решим однородное уравнение
или Переходя к переменной у, решим уравнение Будем искать частное решение исходного неоднородного дифференциального уравнения в виде:
где
Для уравнений второго порядка
Так как
Таким образом, частное решение исходного неоднородного уравнения будет иметь вид:
а общее его решение
Решение: Продифференцируем первое уравнение системы но t:
Заменяя функцию y ее выражением из первого уравнения системы
приходим к линейному однородному уравнению второго порядка относительно одной неизвестной функции х:
или
Последнее уравнение – это однородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решая характеристическое уравнение
Подставим выражения для х и
Пример 0.13 Решение: Ищем решение данного дифференциального уравнения в виде ряда Маклорена
Подставив в это уравнение первое начальное условие у= 1 при х=0, получим из исходного дифференциального уравнения
При х = 0:
Подставляя найденные значения производных в ряд (4.2.4), для решения у(х) получим приближенное значение в виде частичной суммы ряда
Пример 0.14 Найти кривую, проходящую через точку М(3; 2), для которой отрезок любой ее касательной, заключенный между координатными осями, делится пополам в точке касания. Решение: Как следует из рисунка, иллюстрирующего условие
задачи, точка М есть середина касательной к графику функции
Таким образом уравнение
Используя начальное условие (заданную точку (3, 2)), определяем
Пример 0.15. В 1980 году в городе проживало 100000 жителей. В течение последующих лет население города увеличивалось со скоростью, пропорциональной числу жителей в текущий момент времени. В 1990 году в городе проживало уже 120000 жителей. Сколько жителей должно проживать в городе в 2000 году. Решение: Обозначим через t время, прошедшее с момента начала отсчета, т.е. с 1980 года, а через
или
По условию задачи в начальный момент времени
Следовательно частное решение Используя информацию о том. что через 10 лет в 1990 году население города составляло уже 120000 человек, найдем значение коэффициента пропорциональности k. В нашем случае целесообразнее искать
Таким образом закон, по которому менялось число жителей города, следующий:
Используя установленный закон, найдем, что в 2000 году (t=20) в городе может проживать:
ВАРИАНТЫ ЗАДАНИЙ
ВАРИАНТ 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 1.11 1.12 1.13 1.14 Найти линию, у которой любая касательная пересекается с осью ординат в точке, одинаково удаленной от точки касания и от начала координат. 1.15 Через сколько времени температура тела, нагретого до 100°, понизится до 30°, если температура помещения 20° и за первые 20 минут тело охладилось до 60°. По закону охлаждения Ньютона скорость охлаждения тела пропорциональна разности температур тела и окружающей его среды.
ВАРИАНТ 2 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 2.10 2.11 2.12 2.13 2.14 Найти линию, у которой начальная ордината любой касательной на две единицы масштаба меньше абсциссы точки касания. 2.15 На сколько увеличится длина шнура под действием его веса, если подвесить шнур за один конец. Вес шнура Р, его длина l. Согласно закону Гука эластичный шнур длины I под действием растягивающей силы F получает приращение длины
ВАРИАНТ 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 3.10 3.11 3.12 3.13 3.14 Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания. 3.15 Скорость распада радия пропорциональна наличному количеству его. По истечении 1600 лет остается половина первоначального запаса радия. Найти, какой процент радия окажется распавшимся по истечении 100 лет.
ВАРИАНТ 4 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 4.10 4.11 4.12 4.13 4.14 Найти линию, у которой длина нормали есть постоянная величина а. 4.15 Если при прохождении через слой воды толщиной 3 метра поглощается половина первоначального количества света, то какая часть этого количества света дойдет до глубины 30 метров. Количество света, поглощаемого тонким слоем воды, пропорционально количеству проходящего света и толщине слоя.
ВАРИАНТ 5 5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 5.9 5.10 5.11 5.12 5.13 5.14 Найти линию, проходящую через точку (a, 1) и имеющую постоянную подкасательную, равную а.
5.15 Если через два часа после начала брожения наличное количество фермента составляет 2 грамма, а через три часа 3 грамма, то каково было первоначальное количество фермента, если считать, что скорость прироста фермента, пропорциональна его наличному количеству?
ВАРИАНТ 6 6.1 6.2 6.3 6.4 6.5 6.6 6.7 6.8 6.9 6.10 6.11 6.12 6.13 6.14 Найти кривую, у которой длина нормали в любой ее точке равна расстоянию этой точки от начала координат.
6.15. Какую работу надо затратить чтобы тело массы m с земной поверхности удалить в бесконечность
ВАРИАНТ 7 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8. 7.9 7.10 7.11 7.12 7.13 7.14 Найти кривую, проходящую через точку (0, 1), у которой под-касательная равна сумме координат точки касания.
7.15 Тяжелая цепь длиной 200м поднимается, навиваясь на ворот.Определит] работу, производимую при поднятии цепи, пренебрегая размерами ворота, если погонный метр цепи весит 50кг.
ВАРИАНТ 8 8.1 8.2 8.3 8.4 8.5
|

 го порядка, допускающие понижения порядка; линейные с постоянными коэффициентами; системы линейных уравнений.
го порядка, допускающие понижения порядка; линейные с постоянными коэффициентами; системы линейных уравнений.




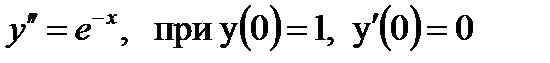





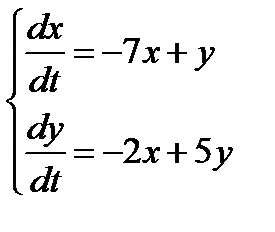



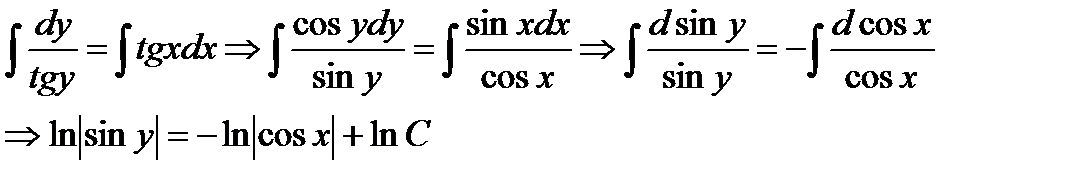
 или окончательно решение дифференциального уравнения имеет вид:
или окончательно решение дифференциального уравнения имеет вид: 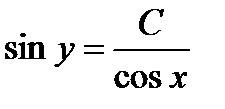

 , решение которых осуществляется подстановкой
, решение которых осуществляется подстановкой  . Отсюда
. Отсюда  ,
,  . После подстановки в дифференциальное уравнение получим:
. После подстановки в дифференциальное уравнение получим:  разделяем переменные
разделяем переменные  интегрируем обе части уравнения
интегрируем обе части уравнения 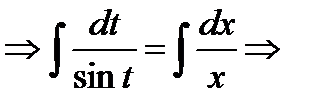 табличные интегралы
табличные интегралы  на основании свойств логарифмов
на основании свойств логарифмов  или
или  .
. , находим общее решение исходного уравнения
, находим общее решение исходного уравнения  .
. , получим:
, получим: 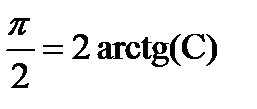 или
или  , т.е. С=1.
, т.е. С=1.
 , которые допускают решения двумя способами:
, которые допускают решения двумя способами:

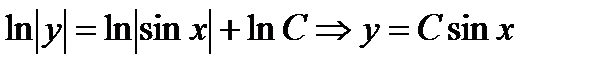
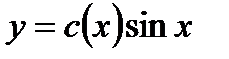 , где с (x) - неизвестная функция. Подставляя в исходное уравнение
, где с (x) - неизвестная функция. Подставляя в исходное уравнение 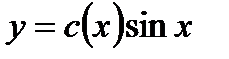 к
к  , перейдем к уравнению:
, перейдем к уравнению: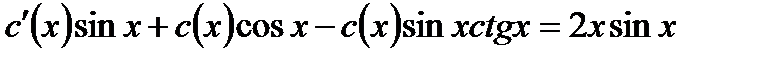


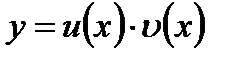 .
. и
и 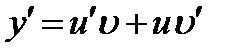 :
: ,
, . (4.2.1)
. (4.2.1) и решаем это дифференциальное уравнение с разделяющимися переменными. Его решение —
и решаем это дифференциальное уравнение с разделяющимися переменными. Его решение —  . Подставляем найденное значение v в оставшуюся часть уравнения (4.2.1):
. Подставляем найденное значение v в оставшуюся часть уравнения (4.2.1):  и получаем
и получаем 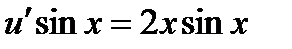 . После сокращения:
. После сокращения:  . Решаем это уравнение с разделяющимися переменными:
. Решаем это уравнение с разделяющимися переменными: 
 ,
,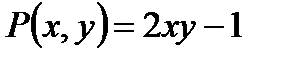 , а
, а 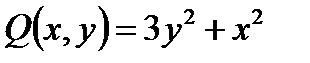 , то
, то  ,
,  , т.е.
, т.е.  . Таким образом данное уравнение является дифференциальным уравнением в полных дифференциалах:
. Таким образом данное уравнение является дифференциальным уравнением в полных дифференциалах: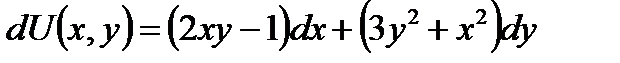 .
. , имеем
, имеем 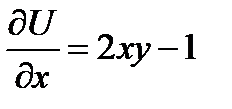 ;
; 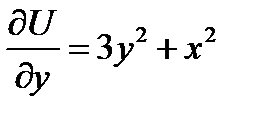
 (4.2.2)
(4.2.2)
 , или
, или .
. в уравнение (4.2.2), окончательно имеем:
в уравнение (4.2.2), окончательно имеем: или
или  .
. , решение которого осуществляется понижением порядка. Подставим в дифференциальное уравнение новую переменную
, решение которого осуществляется понижением порядка. Подставим в дифференциальное уравнение новую переменную  . С учетом того, что
. С учетом того, что 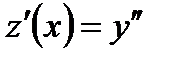 , получим уравнение:
, получим уравнение:  , или
, или  , которое является однородным дифференциальным уравнением первого порядка. Для решения этого уравнения введем еще одну переменную
, которое является однородным дифференциальным уравнением первого порядка. Для решения этого уравнения введем еще одну переменную 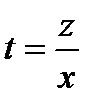 , откуда
, откуда 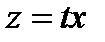 ,
, 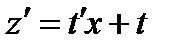 :
: 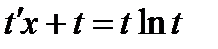 , или
, или 
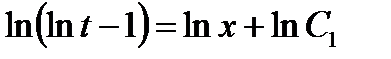 , или
, или 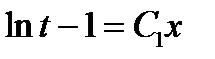 , откуда
, откуда  . Возвращаясь к переменной
. Возвращаясь к переменной  , получим уравнение
, получим уравнение 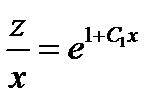 . Переходя окончательно к переменной у, получим уравнение
. Переходя окончательно к переменной у, получим уравнение
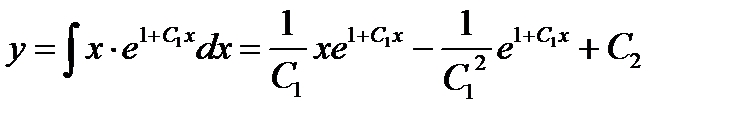
 , при этом
, при этом 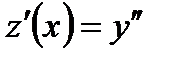 . Полученное уравнение
. Полученное уравнение 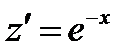 является уравнением с разделяющимися переменными, решение которого:
является уравнением с разделяющимися переменными, решение которого: 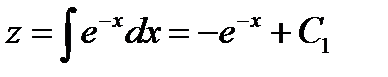 Перейдя к исходной переменной у окончательно будем иметь общее решение дифференциального уравнения
Перейдя к исходной переменной у окончательно будем иметь общее решение дифференциального уравнения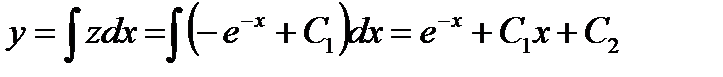
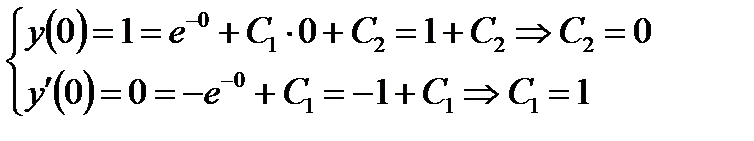
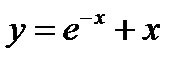

 , допускающее понижение порядка. Введем новую неизвестную функцию
, допускающее понижение порядка. Введем новую неизвестную функцию  , полагая
, полагая  . В этом случае
. В этом случае  . Подставив
. Подставив  и
и  в исходное уравнение получим:
в исходное уравнение получим:  . Разделим переменные:
. Разделим переменные:  . Проинтегрируем:
. Проинтегрируем: 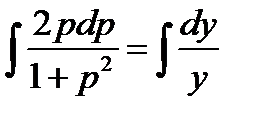 . Отсюда найдем:
. Отсюда найдем:  , или
, или 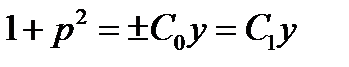 , или
, или  .
. , то
, то 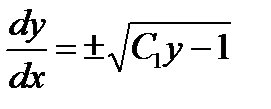 , или
, или 
 , или
, или

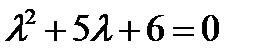 . Его корни
. Его корни  ,
,  . Фундаментальная система частных решений
. Фундаментальная система частных решений  ,
, 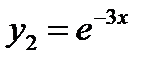 . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид:  .
. , где у - общее решение уравнения без правой части, а
, где у - общее решение уравнения без правой части, а 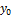 -частное решение уравнения с правой частью. Составляем характеристическое уравнение для однородного дифференциального уравнения
-частное решение уравнения с правой частью. Составляем характеристическое уравнение для однородного дифференциального уравнения  :
:  .
. ,
, 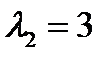 . Общее решение дифференциального уравнения без правой части имеет вид:
. Общее решение дифференциального уравнения без правой части имеет вид:  .
. . В этом случае частное решение
. В этом случае частное решение  следует искать в виде
следует искать в виде  . где r — число корней характеристического уравнения, совпадающих с коэффициентом а в показателе степени показательной функции. В нашем примере
. где r — число корней характеристического уравнения, совпадающих с коэффициентом а в показателе степени показательной функции. В нашем примере 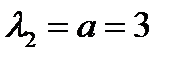 , следовательно,
, следовательно,  , и частное решение
, и частное решение 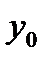 можно записать в виде
можно записать в виде
 и
и  :
: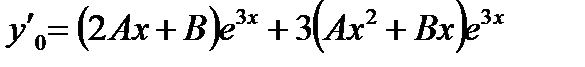

 ,
, 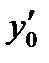 ,
, 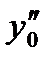 в исходное уравнение и сокращая на множитель
в исходное уравнение и сокращая на множитель 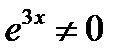 , получаем тождество:
, получаем тождество:


 ,
, 
 , найдем частное решение исходного дифференциального уравнения
, найдем частное решение исходного дифференциального уравнения

 ,
,  . Находим его корни
. Находим его корни  ,
, 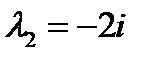 . Общее решение дифференциального уравнения без правой части имеет вид:
. Общее решение дифференциального уравнения без правой части имеет вид: .
.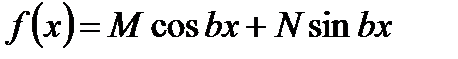 . В этом случае частное решение
. В этом случае частное решение  следует искать в виде:
следует искать в виде: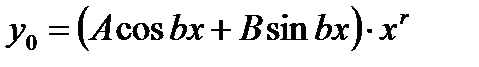 ,
, совпадает с одним из корней характеристического уравнения и, следовательно, r = 1. Будем искать частное решение неоднородного уравнения в форме:
совпадает с одним из корней характеристического уравнения и, следовательно, r = 1. Будем искать частное решение неоднородного уравнения в форме: .
. и
и  :
: ,
, Подставляя выражения для
Подставляя выражения для  ,
,  ,
,  в исходное уравнение, получим:
в исходное уравнение, получим: После приведения подобных членов
После приведения подобных членов .
.
 и общее решение неоднородного уравнения запишется в виде:
и общее решение неоднородного уравнения запишется в виде:
 . Это дифференциальное уравнение второго порядка типа
. Это дифференциальное уравнение второго порядка типа  , следовательно
, следовательно  . После подстановки новой переменной в однородное уравнение будем иметь
. После подстановки новой переменной в однородное уравнение будем иметь  , или разделяя переменные, получим
, или разделяя переменные, получим  . Интегрируя последнее уравнение получим
. Интегрируя последнее уравнение получим или
или 

 , разделим переменные
, разделим переменные  , интегрируем
, интегрируем 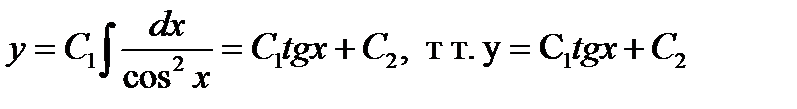

 и
и  неизвестные произвольные постоянные, а
неизвестные произвольные постоянные, а  и
и 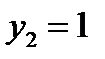 два частных решения однородного дифференциального уравнения, образующие фундаментальную систему решения, так как определитель Вронского для них,
два частных решения однородного дифференциального уравнения, образующие фундаментальную систему решения, так как определитель Вронского для них, .
. , соответствующая система линейных алгебраических уравнений относительно неизвестных произвольных постоянных
, соответствующая система линейных алгебраических уравнений относительно неизвестных произвольных постоянных  и
и  может быть записана в виде
может быть записана в виде

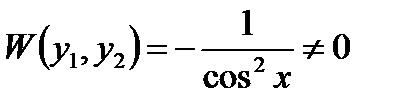 , единственное решение указанных систем можно найти, используя готовые формулы
, единственное решение указанных систем можно найти, используя готовые формулы


 . Подставим в полученное уравнение значение
. Подставим в полученное уравнение значение  из второго уравнения системы:
из второго уравнения системы: .
. , (4.2.3)
, (4.2.3)
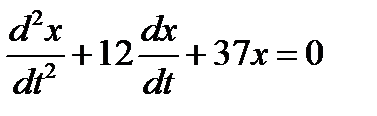
 находим корни
находим корни 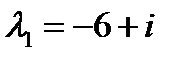 и
и  . Таким образом, общее решение дифференциального уравнения
. Таким образом, общее решение дифференциального уравнения  . Дифференцируя последнее уравнение по t. находим:
. Дифференцируя последнее уравнение по t. находим: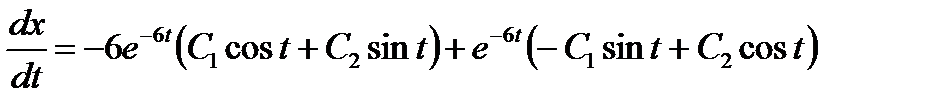
 в равенство (4.2.3) и приведем подобные
в равенство (4.2.3) и приведем подобные Функции
Функции
 являются решением данной системы.
являются решением данной системы.
 (4.2.4)
(4.2.4)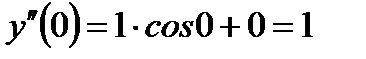 Продифференцируем обе части исходного дифференциального уравнения:
Продифференцируем обе части исходного дифференциального уравнения:


 . Следовательно
. Следовательно  , а
, а  . Угловой коэффициент касательной к кривой
. Угловой коэффициент касательной к кривой 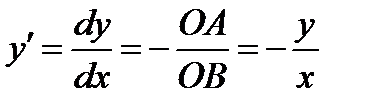
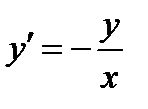 есть дифференциальное уравнение искомой кривой. Это уравнение с разделяющимися переменными. Решая его, найдем:
есть дифференциальное уравнение искомой кривой. Это уравнение с разделяющимися переменными. Решая его, найдем:
 . Итак искомая кривая это гипербола
. Итак искомая кривая это гипербола  .
. - число жителей в момент времени t. Согласно условию задачи уравнение, описывающее изменение числа жителей
- число жителей в момент времени t. Согласно условию задачи уравнение, описывающее изменение числа жителей  , где k - коэффициент пропорциональности прироста населения. Решаем дифференциальное уравнение с разделяющимися переменными:
, где k - коэффициент пропорциональности прироста населения. Решаем дифференциальное уравнение с разделяющимися переменными: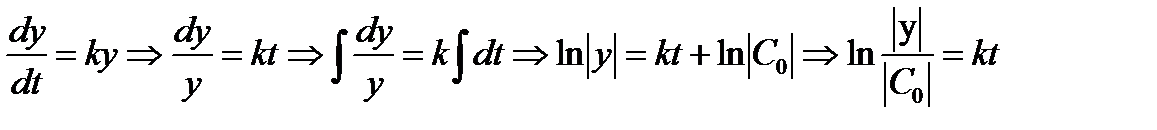
 , или
, или  , или
, или . (4.2.5)
. (4.2.5) население города
население города 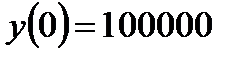 . Подставим начальное условие в уравнение (4.2.5)
. Подставим начальное условие в уравнение (4.2.5) .
. .
. :
:

 человек.
человек.

 , (линейно относительно х)
, (линейно относительно х)