Векторная диаграмма асинхронного двигателя
Для построения векторной диаграммы необходимо определить ток ротора. ЭДС ротора была определена ранее. Полное сопротивление обмотки ротора составляется из активного сопротивления обмотки
где Из ранее полученных соотношений
При неподвижном роторе скольжение равно единице (
Для подаваемого на статор напряжения
Учитывая введенное понятие тока ротора, приведенного к статорной обмотке:
где
По приведенным формулам можно достаточно просто построить векторную диаграмму асинхронного двигателя с неподвижным ротором Векторная диаграмма напряжений ротора построена в соответствии с уравнением
Реактивное сопротивление ротора, обусловленное индуктивностью рассеяния, является величиной положительной, поэтому ток заторможенного ротора Векторная диаграмма напряжений статорной обмотки построена по уравнению
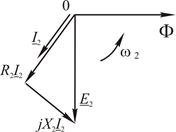
Вектор падения напряжения на сопротивлении обмотки статора Приведенная диаграмма построена для одной из фазных обмоток. Из диаграммы следует, что асинхронный двигатель с короткозамкнутым ротором может рассматриваться как трансформатор с короткозамкнутыми выходными обмотками. Построение векторной диаграммы работающего двигателя затруднено, так как частота тока статора отлична от частоты тока ротора. В этом случае возможно построение отдельно векторной диаграммы напряжений статора (рис. 6.26) и векторной диаграммы ротора (рис. 6.27).
Рис. 6.26 Рис. 6.27
В качестве базового можно использовать вектор магнитного потока, так как относительно статора он вращается со скоростью, определенной частотой тока статора, а относительно ротора частота его вращения совпадает с частотой тока ротора. Относительно обмотки статора магнитный поток изменяется синусоидально во времени с частотой Приведенные векторные диаграммы статорной и роторной цепи построены в соответствии с формулами
Ток ротора выражается через параметры вторичной обмотки следующим образом:
Уравнение показывает, что величину тока ротора можно выразить через электродвижущую силу неподвижного ротора, имеющую частоту
В этом случае соотношения в роторной цепи будут идентичны соотношениям во вторичной обмотке трансформатора, в которой наводится электродвижущая сила
Таким образом, учитывая полученные соотношения, мы можем построить общую векторную диаграмму обеих цепей машины лишь для воображаемого неподвижного ротора, нагруженного на сопротивление
и
|

 и индуктивного сопротивления
и индуктивного сопротивления 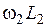 . Сопротивление ротора, таким образом
. Сопротивление ротора, таким образом ,
, ,
,  ,
,  .
. . Следовательно,
. Следовательно, .
. ), и ток неподвижного ротора будет равен
), и ток неподвижного ротора будет равен .
. ЭДС ротора определяется падением напряжения
ЭДС ротора определяется падением напряжения ;
;  .
.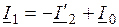 ,
, .
. Рис. 6.25
Рис. 6.25
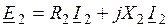 .
. отстает от ЭДС
отстает от ЭДС  на угол
на угол  . Ток статорной обмотки может быть представлен векторной суммой тока холостого хода
. Ток статорной обмотки может быть представлен векторной суммой тока холостого хода  и тока ротора, приведенного к обмотке статора
и тока ротора, приведенного к обмотке статора  , взятого со знаком минус. Коэффициентом приведения тока обмотки ротора к обмотке статора является отношение
, взятого со знаком минус. Коэффициентом приведения тока обмотки ротора к обмотке статора является отношение  , где
, где  и
и  есть количество витков обмотки статора и ротора, а коэффициен-ты
есть количество витков обмотки статора и ротора, а коэффициен-ты  и
и  , всегда меньшие единицы, зависят от способа намотки обмоток статора и ротора соответственно.
, всегда меньшие единицы, зависят от способа намотки обмоток статора и ротора соответственно. .
.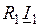 совпадает с током по фазе, а вектор падения напряжения на реактивном сопротивлении рассеяния
совпадает с током по фазе, а вектор падения напряжения на реактивном сопротивлении рассеяния 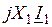 опережает вектор тока на 90 °.
опережает вектор тока на 90 °.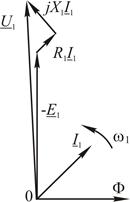
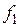 , а относительно ротора с частотой
, а относительно ротора с частотой  .
.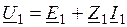 ,
,  ,
, ,
,  .
.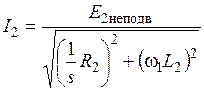 .
. . Эту величину можно рассматривать как сумму реального сопротивления обмотки ротора
. Эту величину можно рассматривать как сумму реального сопротивления обмотки ротора 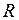 , величина которого зависит от
, величина которого зависит от 
 .
. Рис. 6.28
Рис. 6.28
 и в которую включен резистор сопротивлением
и в которую включен резистор сопротивлением .
. .
.


