Энергетические процессы асинхронной машины
Важным вопросом при рассмотрении электрических машин любого характера является вопрос энергетических соотношений. Под Таким образом, электромагнитная мощность
Электромагнитная мощность передается на ротор через воздушный зазор с помощью магнитного поля. Потери в магнитопроводе ротора достаточно малы, поэтому потери в роторе практически равны потерям в его обмотке
где Полезная мощность двигателя
Таким образом, для асинхронной машины, работающей в режиме двигателя, имеются следующие соотношения:
Рассмотрим электрическое состояние двигателя с вращающимся и неподвижным ротором. В случае двигателя с вращающимся ротором для одной фазы имеем
можно написать
и Для двигателя с неподвижным ротором, обмотка которого замкнута на сопротивление
или так как
Для двигателя с вращающимся ротором
Отсюда следует вывод о том, что механическая мощность одной фазы ротора может быть выражена электрической мощностью, рассеиваемой в некотором резисторе
и тогда где 6.11. Энергетическая диаграмма асинхронного В предыдущем разделе получены уравнения мощностей асинхронного двигателя, позволяющие понять и оценить распределение потребляемой из сети электрической энергии
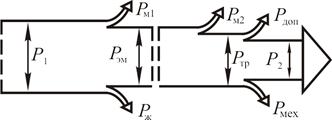
Энергетическая диаграмма, соответствующая этим уравнениям, приведена на рис. 6.31.
Рис. 6.31
Таким образом, потребляемая из сети электрическая мощность а) часть энергии мощностью б) вращающееся магнитное поле приводит к потерям энергии мощностью в) на ротор передается энергия мощностью г) полученная механическая мощность Таким образом, КПД двигателя
6.12. Общее уравнение вращающего момента Если ротор асинхронной машины вращается с циклической частотой
Частота вращения статора
С другой стороны, где
Тогда
где
Как уже утверждалось ранее, механическая мощность, приходящаяся на одну фазу, равна электрической мощности рассеяния в сопротивлении
и где Вращающий момент двигателя в этом случае
Заменим в полученном уравнении
Следовательно,
где В полученном уравнении в явной форме не присутствует частота вращения ротора или скольжение. От скольжения зависят две величины. Увеличение скольжения вызывает быстрое увеличение тока ротора
После первого быстрого увеличения тока темп его увеличения замедляется, так как первая слагаемая подкоренного выражения становится малой и не оказывает существенного влияния на изменение знаменателя. От скольжения зависит и коэффициент мощности роторной цепи
При увеличении скольжения от нуля до 1 Из полученных формул следует: а) при практически постоянном магнитном потоке машины ток ротора увеличивается лишь на участке небольших скольжений, т. е. при частотах вращения, близких к синхронной; б) в) из первых двух заключений при изменении скольжения следует ожидать возрастание механического момента на валу при уменьшении скольжения и последующее его уменьшение при больших значениях Все приведенные выводы объясняются изменением частоты тока ротора при изменении его скорости вращения и изменения соотношения активного и реактивного сопротивления обмотки ротора. Первое остается практически постоянной, а второе прямо пропорционально частоте тока ротора.
|

 будем понимать активную электрическую мощность, потребляемую двигателем. Одна часть этой мощности
будем понимать активную электрическую мощность, потребляемую двигателем. Одна часть этой мощности  рассеивается омическим сопротивлением обмотки статора, т. е. идет на ее нагревание. Вторая часть расходуется на создание вращающегося магнитного поля. Вращающееся магнитное поле, перемагничивая магнитопровод машины, состоящий из магнитопровода статора и ротора, приводит к потерям в магнитопроводе, учитываемым мощностью
рассеивается омическим сопротивлением обмотки статора, т. е. идет на ее нагревание. Вторая часть расходуется на создание вращающегося магнитного поля. Вращающееся магнитное поле, перемагничивая магнитопровод машины, состоящий из магнитопровода статора и ротора, приводит к потерям в магнитопроводе, учитываемым мощностью 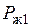 . Эта мощность учитывает только потери в магнитопроводе статора, так как частота тока ротора
. Эта мощность учитывает только потери в магнитопроводе статора, так как частота тока ротора  очень мала и мала скорость перемагничивания стали ротора, что обеспечивает малые потери на перемагничивание и на вихревые токи.
очень мала и мала скорость перемагничивания стали ротора, что обеспечивает малые потери на перемагничивание и на вихревые токи.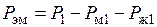 .
. ,
,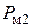 - мощность потерь на нагревание обмотки ротора.
- мощность потерь на нагревание обмотки ротора. меньше механической мощности
меньше механической мощности  , так как, кроме потерь в обмотке ротора
, так как, кроме потерь в обмотке ротора 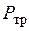 и дополнительные потери
и дополнительные потери 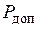
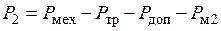 .
.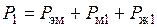 ,
, 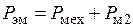 ,
, 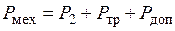 .
.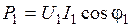 ;
;  ;
; 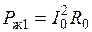 ;
; 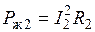 ;
;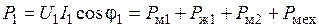
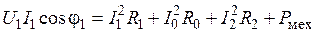 .
.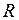 , имеем
, имеем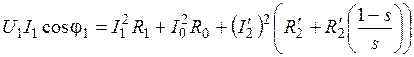 ;
;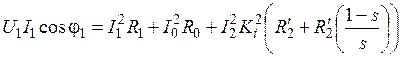 ,
, и
и 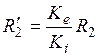 , где
, где 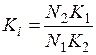 и
и 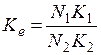 , и тогда
, и тогда 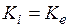 или
или 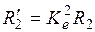 . Учитывая это, преобразуем уравнение:
. Учитывая это, преобразуем уравнение: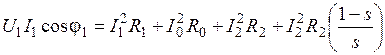 .
.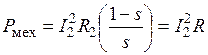 .
. . Можно добавить и то, что если пренебречь потерями в магнитопроводе ротора машины, электромагнитная мощность равна сумме механической мощности и мощности потерь в обмотке ротора
. Можно добавить и то, что если пренебречь потерями в магнитопроводе ротора машины, электромагнитная мощность равна сумме механической мощности и мощности потерь в обмотке ротора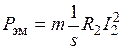 или
или 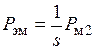 ;
; 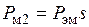 ,
,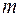 - число фаз ротора.
- число фаз ротора.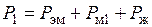 ,
,
 на перемагничивание и на вихревые токи в магнитопроводе машины;
на перемагничивание и на вихревые токи в магнитопроводе машины;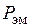 . Но не вся электромагнитная энергия превращается в механическую энергию, так как на нагревание обмотки ротора затрачивается энергия мощностью
. Но не вся электромагнитная энергия превращается в механическую энергию, так как на нагревание обмотки ротора затрачивается энергия мощностью 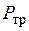 и на дополнительные потери, вызываемые потерями на вентиляцию двигателя и на трение ротора о воздух.
и на дополнительные потери, вызываемые потерями на вентиляцию двигателя и на трение ротора о воздух.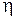 вычисляется по уравнению:
вычисляется по уравнению: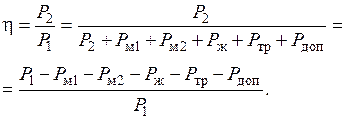
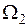 , а вращающий момент, создаваемый машиной
, а вращающий момент, создаваемый машиной 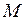 , то
, то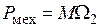 .
. , так как
, так как 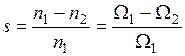 .
. ,
,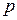 - число пар полюсов машины;
- число пар полюсов машины;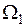 - частота вращения магнитного поля.
- частота вращения магнитного поля.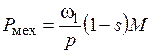 ,
,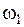 - частота тока сети;
- частота тока сети; - скольжение.
- скольжение.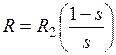 . Тогда в асинхронной машине, имеющей
. Тогда в асинхронной машине, имеющей 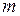 фаз
фаз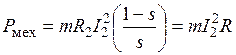
 ,
,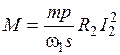 .
.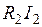 , выражаем
, выражаем 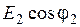 и
и 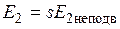 , тогда уравнение для определения механического момента примет вид
, тогда уравнение для определения механического момента примет вид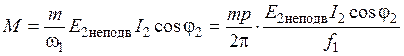 ;
;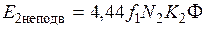 .
.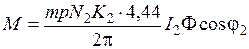 ;
; ,
,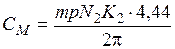 .
. в соответствии с формулой
в соответствии с формулой .
.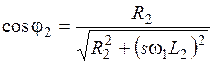 .
. уменьшается сначала медленно, а затем быстро, когда
уменьшается сначала медленно, а затем быстро, когда 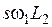 становится гораздо больше, чем
становится гораздо больше, чем  .
.


