Круговая диаграмма дает большие возможности при анализе режимов работы асинхронной машины (рис. 6.37).

Рис. 6.37
Зная величину номинального тока или тока машины, работающего в любом другом режиме, можно найти на окружности рабочую точку (например E), когда отрезок OE будет соответствовать в масштабе рабочему току обмотки статора. Угол между I 1 и U 1 позволит получить коэффициент мощности cosj. Мощность P 1 = mU 1 I 1cosj1 = KI 1cosj. Опуская перпендикуляр из точки E на ось абсцисс, мы получим отрезок Ed = I 1cosj, который пропорционален мощности P 1. Масштаб мощности определяется произведением масштаба тока на величину напряжения U 1, т. е. mP = mU 1 mi, где mP - масштаб мощности, mi - масштаб тока, m - количество фаз.
Масштаб мощности может быть определен из опыта при заторможенном роторе. В соответствии с диаграммой сегмент 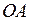 представляет ток двигателя при блокированном роторе и при номинальном напряжении. В соответствии с предыдущими объяснениями длина перпендикуляра, опущенного из точки
представляет ток двигателя при блокированном роторе и при номинальном напряжении. В соответствии с предыдущими объяснениями длина перпендикуляра, опущенного из точки  на ось абсцисс
на ось абсцисс 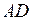 , пропорциональна мощности
, пропорциональна мощности  короткозамкнутой машины, питаемой номинальным напряжением. Но мощность
короткозамкнутой машины, питаемой номинальным напряжением. Но мощность  , потребляемая заторможенным двигателем, является суммарной мощностью потерь в меди и стали машины. С другой стороны, мощность машины, работающей в режиме холостого хода, определяется мощностью потерь в магнитопроводе. На круговой диаграмме отрезок
, потребляемая заторможенным двигателем, является суммарной мощностью потерь в меди и стали машины. С другой стороны, мощность машины, работающей в режиме холостого хода, определяется мощностью потерь в магнитопроводе. На круговой диаграмме отрезок  пропорционален этой мощности. Тогда длина отрезка
пропорционален этой мощности. Тогда длина отрезка  пропорциональна мощности потерь в проводе короткозамкнутой машины.
пропорциональна мощности потерь в проводе короткозамкнутой машины.
Разделим отрезок 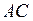 , отражающий потери в меди машины, работающей в режиме короткого замыкания пропорционально величинам
, отражающий потери в меди машины, работающей в режиме короткого замыкания пропорционально величинам  и
и  . Необходимо напомнить о том, что
. Необходимо напомнить о том, что  . Отрезок
. Отрезок 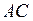 разделен точкой
разделен точкой  на два отрезка. Длина первого отрезка
на два отрезка. Длина первого отрезка  пропорциональна мощности потерь в проводе обмотки статора, и отрезок
пропорциональна мощности потерь в проводе обмотки статора, и отрезок  отражает потери в обмотке ротора. Перед определением потерь в машине, скольжение которой не равняется нулю, необходимо уточнить общие зависимости.
отражает потери в обмотке ротора. Перед определением потерь в машине, скольжение которой не равняется нулю, необходимо уточнить общие зависимости.
Если скольжение  , что соответствует неподвижному ротору, то
, что соответствует неподвижному ротору, то  . Вектор тока
. Вектор тока  при таком значении скольжения займет положение, совпадающее с прямой O¢ A.
при таком значении скольжения займет положение, совпадающее с прямой O¢ A.
В этом случае фазовый сдвиг напряжения 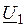 и тока
и тока  определяется из выражения
определяется из выражения
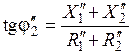 .
.
По векторной диаграмме  , тогда можно записать
, тогда можно записать
 .
.
Таким образом, отрезок  пропорционален сопротивлению
пропорционален сопротивлению  , и
, и 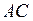 пропорционален сопротивлению
пропорционален сопротивлению  .
.
Треугольники  и
и  подобны и можно написать
подобны и можно написать
 и
и  .
.
Для углов  и
и  , которые образованы вертикальными линиями
, которые образованы вертикальными линиями  и
и 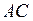
 и
и  ;
;
используя уравнения
 и
и  ,
,
получают
 ;
;
 и
и  ;
;
 ;
;
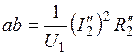 .
.
Таким образом, отрезки  и
и  могут рассматриваться как мощности потерь в меди асинхронной машины. Отрезок
могут рассматриваться как мощности потерь в меди асинхронной машины. Отрезок  выражает потери асинхронной машины, работающей в режиме идеального холостого хода. Можно сказать, что отрезок
выражает потери асинхронной машины, работающей в режиме идеального холостого хода. Можно сказать, что отрезок  выражает мощность машины
выражает мощность машины  . С другой стороны, P эм = P 1 - P ж - P м =
. С другой стороны, P эм = P 1 - P ж - P м =
= P 1 - (P ж + P м) и отрезок bd выражает электромагнитную мощность машины 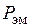 . Тот же отрезок выражает механический момент, так как
. Тот же отрезок выражает механический момент, так как
 .
.
Линия  называется линией моментов, а линия - линией полной механической мощности, так как
называется линией моментов, а линия - линией полной механической мощности, так как  , и эта мощность выражается отрезком
, и эта мощность выражается отрезком 
 .
.
Ранее было показано, что
 ;
;
 ,
,
тогда
 .
.
Проведем касательную  к окружности в точке
к окружности в точке  при скольжении
при скольжении  и прямую
и прямую  параллельно
параллельно  , выражающую электромагнитную мощность
, выражающую электромагнитную мощность 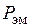 (рис. 6.38).
(рис. 6.38).

Рис. 6.38
Треугольники  и
и 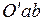 подобны, так как две их стороны параллельны, а третья общая
подобны, так как две их стороны параллельны, а третья общая
 .
.
По той же причине треугольник  подобен треугольнику
подобен треугольнику  , следовательно,
, следовательно,
 .
.
Умножая полученные уравнения, получаем:
 и
и 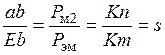 .
.
Отрезок 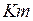 в масштабе дает скольжение машины, работающей
в масштабе дает скольжение машины, работающей
в режиме двигателя. Если провести линию скольжения 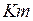 в две стороны и разделить линию с таким же масштабом, что и отре-
в две стороны и разделить линию с таким же масштабом, что и отре-
зок 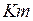 справа от точки
справа от точки 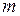 получают величину скольжения
получают величину скольжения  ,
,
а слева от точки  получают скольжение
получают скольжение  .
.
Для учета механических потерь проводят вектор тока машины, работающей в реальном режиме холостого хода  (рис. 6.39).
(рис. 6.39).

Рис. 6.39
Проводят линию  . Отрезок
. Отрезок  выражает механические потери асинхронного двигателя, работающего в реальном режиме холостого хода. Используя линию
выражает механические потери асинхронного двигателя, работающего в реальном режиме холостого хода. Используя линию  , можно построить линию коэффициента полезного действия. Продлив линию
, можно построить линию коэффициента полезного действия. Продлив линию  до пересечения с осью абсцисс в точке
до пересечения с осью абсцисс в точке 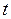 , через точку
, через точку 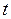 проводят прямую
проводят прямую  , параллельную оси ординат. Проведем прямую
, параллельную оси ординат. Проведем прямую  параллельно оси абсцисс. Треугольник
параллельно оси абсцисс. Треугольник  подобен треугольнику
подобен треугольнику  , так как две стороны треугольника параллельны, а третья находится на общей линии. Тогда
, так как две стороны треугольника параллельны, а третья находится на общей линии. Тогда
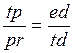 .
.
Треугольники  и
и  подобны по тем же признакам, и тогда
подобны по тем же признакам, и тогда
 .
.
Умножая полученные уравнения, получают следующую пропорцию:

или  и
и 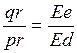 .
.
Мы установили, что КПД машины, работающей в режиме двигателя,
 .
.
Это значит, что отрезок  отражает в определенном масштабе КПД асинхронной машины, работающей в режиме двигателя.
отражает в определенном масштабе КПД асинхронной машины, работающей в режиме двигателя.


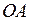 представляет ток двигателя при блокированном роторе и при номинальном напряжении. В соответствии с предыдущими объяснениями длина перпендикуляра, опущенного из точки
представляет ток двигателя при блокированном роторе и при номинальном напряжении. В соответствии с предыдущими объяснениями длина перпендикуляра, опущенного из точки  на ось абсцисс
на ось абсцисс 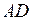 , пропорциональна мощности
, пропорциональна мощности  короткозамкнутой машины, питаемой номинальным напряжением. Но мощность
короткозамкнутой машины, питаемой номинальным напряжением. Но мощность  пропорционален этой мощности. Тогда длина отрезка
пропорционален этой мощности. Тогда длина отрезка  пропорциональна мощности потерь в проводе короткозамкнутой машины.
пропорциональна мощности потерь в проводе короткозамкнутой машины.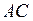 , отражающий потери в меди машины, работающей в режиме короткого замыкания пропорционально величинам
, отражающий потери в меди машины, работающей в режиме короткого замыкания пропорционально величинам  и
и  . Необходимо напомнить о том, что
. Необходимо напомнить о том, что  . Отрезок
. Отрезок  на два отрезка. Длина первого отрезка
на два отрезка. Длина первого отрезка  пропорциональна мощности потерь в проводе обмотки статора, и отрезок
пропорциональна мощности потерь в проводе обмотки статора, и отрезок  отражает потери в обмотке ротора. Перед определением потерь в машине, скольжение которой не равняется нулю, необходимо уточнить общие зависимости.
отражает потери в обмотке ротора. Перед определением потерь в машине, скольжение которой не равняется нулю, необходимо уточнить общие зависимости. , что соответствует неподвижному ротору, то
, что соответствует неподвижному ротору, то  . Вектор тока
. Вектор тока  при таком значении скольжения займет положение, совпадающее с прямой O¢ A.
при таком значении скольжения займет положение, совпадающее с прямой O¢ A.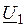 и тока
и тока 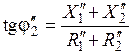 .
. , тогда можно записать
, тогда можно записать .
. пропорционален сопротивлению
пропорционален сопротивлению  , и
, и  .
. и
и  подобны и можно написать
подобны и можно написать и
и  .
. и
и  , которые образованы вертикальными линиями
, которые образованы вертикальными линиями  и
и  и
и  ;
; и
и  ,
, ;
; и
и  ;
; ;
;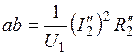 .
. и
и  могут рассматриваться как мощности потерь в меди асинхронной машины. Отрезок
могут рассматриваться как мощности потерь в меди асинхронной машины. Отрезок  выражает потери асинхронной машины, работающей в режиме идеального холостого хода. Можно сказать, что отрезок
выражает потери асинхронной машины, работающей в режиме идеального холостого хода. Можно сказать, что отрезок  выражает мощность машины
выражает мощность машины  . С другой стороны, P эм = P 1 - P ж - P м =
. С другой стороны, P эм = P 1 - P ж - P м =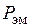 . Тот же отрезок выражает механический момент, так как
. Тот же отрезок выражает механический момент, так как .
. называется линией моментов, а линия - линией полной механической мощности, так как
называется линией моментов, а линия - линией полной механической мощности, так как  , и эта мощность выражается отрезком
, и эта мощность выражается отрезком 
 .
. ;
; ,
, .
. к окружности в точке
к окружности в точке  при скольжении
при скольжении  и прямую
и прямую  параллельно
параллельно  , выражающую электромагнитную мощность
, выражающую электромагнитную мощность 
 и
и 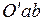 подобны, так как две их стороны параллельны, а третья общая
подобны, так как две их стороны параллельны, а третья общая .
. подобен треугольнику
подобен треугольнику  , следовательно,
, следовательно, .
. и
и 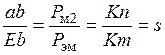 .
.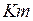 в масштабе дает скольжение машины, работающей
в масштабе дает скольжение машины, работающей 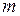 получают величину скольжения
получают величину скольжения  ,
,  получают скольжение
получают скольжение  .
. (рис. 6.39).
(рис. 6.39).
 . Отрезок
. Отрезок  выражает механические потери асинхронного двигателя, работающего в реальном режиме холостого хода. Используя линию
выражает механические потери асинхронного двигателя, работающего в реальном режиме холостого хода. Используя линию 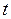 , через точку
, через точку  , параллельную оси ординат. Проведем прямую
, параллельную оси ординат. Проведем прямую  параллельно оси абсцисс. Треугольник
параллельно оси абсцисс. Треугольник  подобен треугольнику
подобен треугольнику  , так как две стороны треугольника параллельны, а третья находится на общей линии. Тогда
, так как две стороны треугольника параллельны, а третья находится на общей линии. Тогда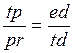 .
. и
и  подобны по тем же признакам, и тогда
подобны по тем же признакам, и тогда .
.
 и
и 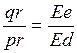 .
. .
. отражает в определенном масштабе КПД асинхронной машины, работающей в режиме двигателя.
отражает в определенном масштабе КПД асинхронной машины, работающей в режиме двигателя.


