Эксплуатационные и другие характеристики асинхронных машин могут быть найдены с помощью испытаний нагруженной машины. Но проведение испытаний не всегда реализуемо. В этом случае характеристики получают с помощью круговых диаграмм, которые могут быть построены по результатам испытаний машины в режиме холостого хода и при заторможенном роторе.
Рассмотрим схему эквивалентной цепи, представленной
на рис. 6.34. Ток намагничивающей цепи при постоянном входном напряжении  остается неизменным при всех изменениях скольжения или при всех изменениях нагрузки асинхронной машины.
остается неизменным при всех изменениях скольжения или при всех изменениях нагрузки асинхронной машины.
Чтобы получить вектор входного тока  , необходимо геометрически сложить независимый от скольжения вектор намагничивающего тока
, необходимо геометрически сложить независимый от скольжения вектор намагничивающего тока  с изменяющимся вектором главной цепи
с изменяющимся вектором главной цепи  , который зависит от скольжения
, который зависит от скольжения
 .
.
В соответствии со схемой замещения
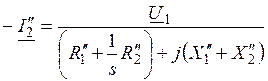 ,
,
откуда
 ;
;
разделив уравнение на 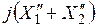 , получаем:
, получаем:
 ;
;
 .
.
Рассмотрим полученные уравнения с точки зрения изменения скольжения асинхронной машины.
Вектор левой части не зависит от скольжения и расположен под 90 ° по отношению к вектору 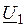 , первое слагаемое правой части равно нулю, при условии
, первое слагаемое правой части равно нулю, при условии
 ,
,
т. е. тогда, когда скольжение
 ;
;
и в этом случае
 .
.
С другой стороны, это слагаемое отстает от тока  на угол в 90 °.
на угол в 90 °.
В результате сложения получаем результирующий вектор
 ,
,
 Рис. 6.35
Рис. 6.35
|
который не зависит от скольжения. Перечисленные векторы образуют прямоугольный треугольник, катетами которого являются векторы  (катет OE) и
(катет OE) и  (катет EL), длины которых изменяются с изменением скольжения, а гипотенуза OL, пропорциональная вектору
(катет EL), длины которых изменяются с изменением скольжения, а гипотенуза OL, пропорциональная вектору
 ,
,
остается неизменной (рис. 6.35).
При изменении скольжения конец вектора  опишет окружность. Добавляя к вектору
опишет окружность. Добавляя к вектору  вектор
вектор  , получим входной ток двигателя
, получим входной ток двигателя  . При изменении скольжения конец вектора
. При изменении скольжения конец вектора  будет скользить по той же окружности. Полученная таким образом геометрическая фигура позволяет определить изменение модуля тока сети питания и его фазового сдвига относительно входного напряжения.
будет скользить по той же окружности. Полученная таким образом геометрическая фигура позволяет определить изменение модуля тока сети питания и его фазового сдвига относительно входного напряжения.
На рис. 6.36 представлена круговая диаграмма асинхронного двигателя. Диаметр окружности определен вектором  , длина которого пропорциональна напряжению и зависит от параметров двигателя
, длина которого пропорциональна напряжению и зависит от параметров двигателя
 .
.
Нами получена векторная диаграмма асинхронной машины. Она может быть построена по известным значениям тока холостого хода и тока двигателя при заторможенном роторе. Ток холостого хода и ток заторможенного двигателя могут быть определены теоретически или экспериментально (см. рис. 6.36).
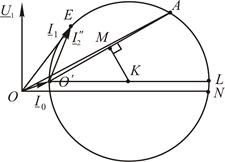
Рис. 6.36
Для определения  необходимо подключить машину к сети питания при отсутствии нагрузки и измерить входное напряже-
необходимо подключить машину к сети питания при отсутствии нагрузки и измерить входное напряже-
ние  , ток холостого хода
, ток холостого хода  и активную мощность
и активную мощность 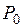 . По полученным значениям определяют коэффициент мощности и фазовый сдвиг напряжения и тока
. По полученным значениям определяют коэффициент мощности и фазовый сдвиг напряжения и тока
 ,
,
таким образом  . На круговой диаграмме ток холостого хода представлен отрезком OO¢.
. На круговой диаграмме ток холостого хода представлен отрезком OO¢.
Для определения тока короткого замыкания  , ротор машины должен быть заторможен, а обмотка ротора закорочена, если испытывается машина с фазным ротором. На статорную обмотку подается небольшое напряжение, при котором ток обмотки статора будет равен номинальному значению
, ротор машины должен быть заторможен, а обмотка ротора закорочена, если испытывается машина с фазным ротором. На статорную обмотку подается небольшое напряжение, при котором ток обмотки статора будет равен номинальному значению 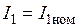 . При номинальном токе первичной обмотки измеряют напряжение
. При номинальном токе первичной обмотки измеряют напряжение  и мощность короткого замыкания
и мощность короткого замыкания  . Фазовый сдвиг тока короткого замыкания и напряжения определяются из формулы
. Фазовый сдвиг тока короткого замыкания и напряжения определяются из формулы
 .
.
Ток короткого замыкания при номинальном напряжении определяется на основании предположения, что ток обмотки статора пропорционален напряжению
 ,
,
где  - напряжение на зажимах двигателя при заторможенном роторе и номинальном токе обмотки статора.
- напряжение на зажимах двигателя при заторможенном роторе и номинальном токе обмотки статора.
Для построения круговой диаграммы выбирают масштаб и строят токи  и
и  , затем проводят прямую
, затем проводят прямую  параллельно оси абсцисс. На этой прямой находится центр окружности. Соединив концы вектора
параллельно оси абсцисс. На этой прямой находится центр окружности. Соединив концы вектора  и
и  , получают отрезок, из середины которого необходимо восстановить перпендикуляр до пересечения с лини-
, получают отрезок, из середины которого необходимо восстановить перпендикуляр до пересечения с лини-
ей O¢ L. Полученная точка K и является центром искомой окружности.

 остается неизменным при всех изменениях скольжения или при всех изменениях нагрузки асинхронной машины.
остается неизменным при всех изменениях скольжения или при всех изменениях нагрузки асинхронной машины. , необходимо геометрически сложить независимый от скольжения вектор намагничивающего тока
, необходимо геометрически сложить независимый от скольжения вектор намагничивающего тока  с изменяющимся вектором главной цепи
с изменяющимся вектором главной цепи  , который зависит от скольжения
, который зависит от скольжения .
.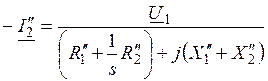 ,
, ;
;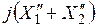 , получаем:
, получаем: ;
; .
.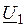 , первое слагаемое правой части равно нулю, при условии
, первое слагаемое правой части равно нулю, при условии ,
, ;
; .
. на угол в 90 °.
на угол в 90 °. ,
, Рис. 6.35
Рис. 6.35
 (катет OE) и
(катет OE) и  (катет EL), длины которых изменяются с изменением скольжения, а гипотенуза OL, пропорциональная вектору
(катет EL), длины которых изменяются с изменением скольжения, а гипотенуза OL, пропорциональная вектору , получим входной ток двигателя
, получим входной ток двигателя  будет скользить по той же окружности. Полученная таким образом геометрическая фигура позволяет определить изменение модуля тока сети питания и его фазового сдвига относительно входного напряжения.
будет скользить по той же окружности. Полученная таким образом геометрическая фигура позволяет определить изменение модуля тока сети питания и его фазового сдвига относительно входного напряжения. , длина которого пропорциональна напряжению и зависит от параметров двигателя
, длина которого пропорциональна напряжению и зависит от параметров двигателя
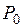 . По полученным значениям определяют коэффициент мощности и фазовый сдвиг напряжения и тока
. По полученным значениям определяют коэффициент мощности и фазовый сдвиг напряжения и тока ,
, . На круговой диаграмме ток холостого хода представлен отрезком OO¢.
. На круговой диаграмме ток холостого хода представлен отрезком OO¢. , ротор машины должен быть заторможен, а обмотка ротора закорочена, если испытывается машина с фазным ротором. На статорную обмотку подается небольшое напряжение, при котором ток обмотки статора будет равен номинальному значению
, ротор машины должен быть заторможен, а обмотка ротора закорочена, если испытывается машина с фазным ротором. На статорную обмотку подается небольшое напряжение, при котором ток обмотки статора будет равен номинальному значению 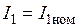 . При номинальном токе первичной обмотки измеряют напряжение
. При номинальном токе первичной обмотки измеряют напряжение  и мощность короткого замыкания
и мощность короткого замыкания  . Фазовый сдвиг тока короткого замыкания и напряжения определяются из формулы
. Фазовый сдвиг тока короткого замыкания и напряжения определяются из формулы .
. ,
, , затем проводят прямую
, затем проводят прямую  и
и 


