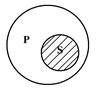
Дайте объединенную классификацию суждений. Изобразите отношения между терминами с помощью круговых схем. Установите распределенность субъекта и предиката
1. Все мелкие предприятия торговли были приватизированы. 2. Некоторые менеджеры не обладают искусством управления коллективом. 3. «Ни один ученый не мыслит формулами». (А.Эйнштейн) 4. Некоторые бизнесмены – меценаты. 5. Все заказчики являются клиентами. 6. Некоторые люди – предприниматели. 7. Не все операции с иностранной валютой законны. 8. Ни один нормальный человек не желает зла другому. 9. Все предприятия, производящие товары народного потребления, имеют льготное налогообложение. 10. Некоторые люди не изучают логику. Примеры: 1. Суждение «Каждый рэкетир есть вымогатель» - общеутвердительное, субъектом (S) является понятие «рэкетир», предикатом (P) – «вымогатель». В данном суждении субъект распределен, и предикат распределен, т.к. их объемы полностью совпадают («рэкетир» и «вымогатель» - синонимы).
2. Суждение: «Все предприниматели платят налоги» - общеутвердительное (A), субъектом (S) является понятие «предприниматели», предикатом (P) – «платят налоги». В данном примере субъект распределен, предикат не распределен, т.к. объем предиката больше объема субъекта (не только предприниматели платят налоги).
3. Суждение: «Ни один честный человек не украдет чужое имущество» - общеотрицательное (Е), субъектом (S) является понятие «честный человек», предикатом (P) – «не украдет чужое имущество». В данном суждении и субъект, и предикат распределены, т.к. объем субъекта полностью исключается из объема предиката и наоборот.
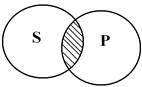
4. Суждение: «Некоторые депутаты Госдумы - экономисты» - частноутвердительное (I), субъектом является понятие «депутаты Госдумы», предикатом – «экономисты». В данном суждении как субъект, так и предикат не взяты в полном объеме, поэтому ни субъект, ни предикат не распределены.
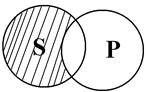
5. Суждение: «Некоторые люди - менеджеры» - частноутвердительное (I), субъектом является понятие «люди», предикатом – «менеджеры». Субъект не распределен, а предикат распределен, т.к. объем предиката полностью входит в объем субъекта.
6. Суждение: «Некоторые миллионеры не являются меценатами» - частноотрицательное (О), субъектом является понятие «миллионеры», предикатом – «меценатами». Субъект не распределен, предикат распределен, ибо в нем мыслятся все меценаты (объем предиката исключается из объема субъекта).
2.20. С помощью логического квадрата установите отношения между суждениями по их истинности в следующих парах: 1. Все предприниматели имеют высшее образование. Ни один предприниматель не имеет высшего образования. 2. Некоторые преподаватели вузов являются профессорами. Все преподаватели вузов являются профессорами. 3. Ни один свидетель не дает истинных показаний. Некоторые свидетели дают истинные показания. 4. Некоторые менеджеры изучают логику. Некоторые менеджеры не изучают логику. 5. Все предприниматели платят налоги. Некоторые предприниматели не платят налоги. 6. Ни одна фирма не держит в секрете свои патенты. Многие фирмы держат в секрете свои патенты. 7. Все историки умеют работать с первоисточниками. Некоторые историки умеют работать с первоисточниками. 8. Ни один благоразумный человек не суеверен. Некоторые благоразумные люди не суеверны. 9. Все невежественные люди тщеславны. Ни один невежественный человек не тщеславен. 10. Некоторые профессора не являются заведующими кафедр. Ни один профессор не является заведующим кафедрой. Примеры: 1. Рассмотрим отношение между двумя совместимыми суждениями: «Все студенты нашей группы сдали логику на «отлично»» и «Некоторые студенты нашей группы сдали логику на «отлично»». Суждения имеют общий предикат; понятия, выражающие субъекты двух таких суждений, также находятся в отношении логического подчинения; первое суждение – общеутвердительное (А) – подчиняющее, второе – частноутвердительное (I) – подчиненное.
 А Е А Е
В отношении подчинения находятся суждения А и I, Е и О. Если А и Е истинны, то истинны и I и О, но не наоборот. Если I и О истинны, то А и Е неопределены. Так, если суждение «Некоторые студенты нашей группы сдали логику на «отлично»» - истинно, то суждение «Все студенты нашей группы сдали логику на «отлично»» - не определено. 2. Рассмотрим отношение между двумя совместимыми суждениями: «Некоторые предприниматели имеют высшее образование» и «Некоторые предприниматели не имеют высшее образование». Суждения имеют один и тот же субъект и предикат. У них одинаковое количество – (объем субъекта) – оба частные. Различаются они только по качеству связки: первое – утвердительное (I), второе – отрицательное (О). Суждения находятся в отношении частичной совместимости (субконтрарности). Поэтому оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно, т.е., оно может быть либо истинным, либо ложным. 3. Рассмотрим отношение между двумя несовместимыми суждениями: «Все депутаты Госдумы - юристы» и «Ни один депутат Госдумы не является юристом». Эти суждения находятся в отношении противоположности (контрарности), поэтому не могут быть одновременно истинными, но могут быть одновременно ложными. В данном случае оба суждения ложны. В другом случае при ложности суждения: «Ни один судья не является юристом» ему противоположное «Все судьи - юристы» - будет истинным. В отношении противоположности находятся суждения А и Е. В отношении несовместимости находятся также противоречащие суждения А и О, Е и I. Так, суждения «Аристотель является создателем формальной логики» и «Аристотель не является создателем формальной логики» находятся в отношении противоречия (контрадикторности). Поэтому эти суждения одновременно не могут быть ни истинными, ни ложными. Если первое суждение истинно, то другое будет обязательно ложным, а при ложности первого второе будет истинным. 2.21. Назовите, к какому виду относятся следующие сложные суждения. Покажите, посредством каких логических связок они образованы и запишите их в виде логических формул: 1. Город Ульяновск стоит на берегу Волги и является областным центром. 2. Фирма разорилась или вследствие плохой организации производства, или по причине серьезных финансовых затруднений. 3. Директор отправится в командировку на поезде или полетит на самолете. 4. Если регулируемые цены отпустить, они будут зависеть от спроса и предложения. 5. Если и только если человек достиг пенсионного возраста, то он имеет право на получение пенсии по возрасту. 6. Фирма купит товар тогда и только тогда, когда будет снижена цена этого товара на 15%. 6. Неверно, что он сдал все экзамены на «отлично». 7. Если между сторонами достигнуто соглашение, то договор считается заключенным. 8. Наша фирма кредитоспособна и конкурентоспособна. 9. Бизнесмен добивался финансового успеха или экономией денег, или выгодным помещением их в банки. 10. В случае, когда наступает инфляция, имеет место снижение жизненного уровня трудящихся. Пример 1: «Этот человек преуспевающий бизнесмен и хороший семьянин» - суждение соединительное, представляет собой конъюнкцию. Ее формула: а Отношение между исходными высказываниями и сложным конъюнктивным суждением по истинности и ложности можно изобразить в виде следующей таблицы, где «и» - означает истинность, а «л» - ложность.
Пример 2: «Товар или удовлетворяет какую-либо потребность, или является вещью, способной обмениваться на другую вещь» - суждение разделительное, в котором входящие в него суждения связаны логическим союзом «или», имеющим неисключительное значение («или А, или В, или то и другое вместе»). Здесь истинность одного высказывания не отрицает истинности другого. Это не строгая, или соединительно-разделительная дизъюнкция. Ее формула: а Таблица истинности нестрогой дизъюнкции:
Пример 3: «Храбрец или сидит в седле, или спит в сырой земле» (Р.Гамзатов) – суждение разделительное, в котором входящие в него суждения связаны логическим союзом «или», имеющим исключительное (дихотомическое) значение. Это строгая, или исключающая дизъюнкция. Ее формула: а Строгая дизъюнкция истинна тогда, когда истинно лишь одно из двух простых суждений. Когда же а и в одновременно истинны, или одновременно ложны, тогда сложное суждение является ложным.
Таблица истинности:
Пример 4: В суждении: «Если на заводе установить новое оборудование, то повысится производительность труда» - два простых суждения связаны между собой импликацией. Формула этого сложного суждения: а Таблица истинности импликации:
Пример 5: В том случае, когда исходные суждения соединяются между собой логическим союзом «если и только если …, то» или «тогда и только тогда, когда …», мы имеем дело с суждениями эквивалентности. Пример: «Этот ученый не завершит свою научную работу, если и только если не будет своевременного финансирования его экспериментов». Формула эквивалентных суждений: если а, то в, и если в, то а. Символическая запись: а Студенты нередко путают суждения эквивалентности с импликацией. Для того чтобы их отличить, нужно помнить, что эквивалентные суждения можно «обернуть», т.е. поменять местами. Например: «Если студент получает повышенную стипендию, - значит, он сдал все экзамены на «отлично»» и «Если студент сдал все экзамены на «отлично», - значит он будет получать повышенную стипендию». Таблица истинности такова:
|





 в. Оно истинно тогда и только тогда, когда истинным является каждый из аргументов, и ложно, когда по крайней мере одно из исходных высказываний ложно.
в. Оно истинно тогда и только тогда, когда истинным является каждый из аргументов, и ложно, когда по крайней мере одно из исходных высказываний ложно. в.
в.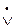 в.
в. в.
в. в.
в.


