Задачи, упражнения и примеры их решения. 11.10. Определите конфликты и возможные способы их разрешения в терминах теории графов в следующих рассуждениях:
11.10. Определите конфликты и возможные способы их разрешения в терминах теории графов в следующих рассуждениях: 1. «У меня болит зуб». 2. Перечислить все возможные способы разрешения конфликта, содержащегося в системе «У меня болит зуб» и указать наиболее вероятные из них. 3. Доказать: «Кто воображает, что то, что он ненавидит, уничтожается, будет чувствовать удовольствие» (Спиноза Б. Избранные произведения Т.1. М., 1957. С.473). Комментарий и пример: Прежде чем приступить к решению задачи, введем несколько предварительных понятий. Линейный граф, или просто граф, состоит из конечного непустого множества неупорядоченных точек А, В, С, …, некоторые пары которого соединены линиями. Неупорядоченные пары точек обозначаются АВ, АС, … Направленный граф, или диграф, есть граф, все или некоторые пары точек которого упорядочены (отображают отношения). Упорядоченные пары точек обозначаются Каждая точка графа или диграфа обозначает некоторый элемент коммуникативной системы – субъекта, вещь, идею, ценность, свойство и т.д. Неупорядоченная пара точек обозначает ненаправленную связь, упорядоченная пара точек – направленную связь. Мы будем называть связь позитивной, если она выражает некоторую форму единства элементов коммуникационной системы – подобие, принадлежность, включенность, симпатию, обладание и т.п. Связь будет называться негативной, если она выражает некоторую форму разъединения элементов. Позитивные связи будут обозначаться знаком «+», негативные связи – знаком «-». Означенный граф, или s-граф, есть граф, некоторые линии которого обозначены как позитивные, а все остальные как негативные. Означенный диграф, или s-диграф, есть диграф, некоторые линии которого обозначены как позитивные, а все остальные как негативные. Примеры графа, диграфа, s-графа, s-диграфа:
- + - + А С А С А + С А - С граф диграф s-граф s-диграф Рис. 1 Путем графа называется множество линий графа вида АВ, ВС, …, DE, где точки А, В, С, …, D, Е различны. Цикл графа состоит из указанного пути вместе с линией ЕА (линией, объединяющей первый и последний элементы пути). Длина цикла равна числу линий в нем. Путем диграфа называется множество упорядоченных линий вида Цикл диграфа состоит из указанного пути вместе с линией Полуциклом диграфа называется множество линий, образованное взятием точно одной линии из каждой пары Каждый цикл необходимо является полуциклом. Полуцикл длиной 2 необходимо образует цикл. Диграф, изображенный на рис. 2, имеет следующие полуциклы: 1. 2. 3. Назовем знаком цикла результат произведения знаков его линий.
Рис. 2 Определение: s-граф сбалансирован, если и только если все его циклы имеют позитивный знак. Рассмотрим следующие четыре s-графа:
А + С А - С А - С А - С а) б) в) г) Рис. 3 Все четыре s-графа, изображенные на рис. 3, имеют один и тот же цикл: АВ, ВС, СА. Вычисление знака каждого из них дает следующий результат: а) (+) б) (+) в) (+) г) (-) Согласно определению баланса s-графа, первые два s-графа на рис.3 сбалансированы, последние два – нет. Определение: s-диграф сбалансирован, если и только если все его полуциклы имеют позитивный знак. Рассмотрим следующие три s-диграфа
- + + - - + - + +
а) б) в) Рис. 4 Каждый из диграфов, изображенных на рис. 4, содержит три полуцикла: 1. 2. 3. Вычисление знаков s-диграфов показывает, что только средний из них сбалансирован. Определим конфликт и возможные способы его разрешения в терминах теории графов в следующем примере: Доказать: «Если мы воображаем, что кто–либо причиняет удовольствие предмету, который мы ненавидим, то мы будем и его ненавидеть. Наоборот, если мы воображаем, что он причиняет этому предмету неудовольствие, мы будем любить его» (Спиноза Б. Избранные произведения. Т.1. С.475). Элементы: А = мы, В = вещь, С = произвольный человек, не принадлежащий к нам. В приведенном рассуждении содержатся две теоремы. Условиями первой являются: А негативно относится к В, С позитивно относится к В. Условиями второй теоремы являются: А негативно относится к В, С негативно относится к В. Первый тезис: А негативно относится к С. Второй тезис: А позитивно относится к С. Иными словами, требуется доказать единственность следующих s-диграфов соответственно:
- + - - А - С А + С Доказательство. Оба s-диграфа имеют один и тот же полуцикл: 11.11. Найдите все возможные способы решения конфликта в баснях И.А.Крылова: 1. «Стрекоза и муравей» 2. «Ворона и лисица». Пример: Найдем все возможные способы разрешения конфликта в басне И.А.Крылова «Ворона и лисица». Элементы: А = Ворона, В = сыр, С = Лисица, s-диграф басни:
+ +
Полуциклы системы и их знаки: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Интерпретация. Вороне сыр нравится, и он ей принадлежит. Лисе сыр также нравится, но он ей не принадлежит. Ворона верит обманным речам Лисы, отношение последней к Вороне негативное, так как содержит умысел отобрать сыр. Возможные способы разрешения конфликта: 1.Знаки линий 2. Знаки линий 3. Знаки 4. Знаки Поскольку общее число способов разрешения конфликта определяется по наибольшему полуциклу, то приведенные способы исчерпывают все возможные варианты.
|

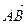 ,
, 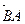 , … В паре
, … В паре 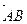 первым элементом является точка В.
первым элементом является точка В.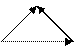
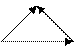

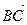 , …,
, …, 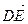 , где точки А, В, С, D, Е различны.
, где точки А, В, С, D, Е различны.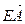 .
.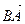 ,
,  , …,
, …, 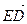 ,
,  .
.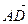 ,
, 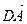 (является циклом).
(является циклом).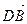 ,
, 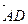 ,
, 


 А В
А В D С
D С
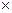 (+)
(+) 

 А + С А - С А - С
А + С А - С А - С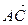 ,
, 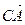
 ,
, 

 В В
В В


 + В -
+ В - +
+ А - С
А - С


