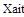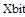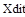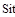Пример выполнения задания методом итераций и методом Зейделя
Решим систему (52) методом итераций.
Сначала запишем систему (52) в нормальном виде, причем постараемся из всех возможных вариантов выбрать такой, чтобы соблюдалось условие (47), т. е. чтобы сумма модулей коэффициентов нормальной системы уравнений по строкам или столбцам была меньше 1:
или
Вариант преобразования 1. 1. Раскроем в уравнениях системы (52) скобки
2. Перенесем в первом уравнении системы (55) член k1tXA вправо, а затем разделим обе части уравнения на k1t. Перенесем во втором уравнении системы (55) член k3tXB вправо, а затем разделим обе части уравнения на k3t. Перенесем в третьем уравнении системы (55) член k4tXD вправо, а затем разделим обе части уравнения на k4t. В левой части уравнений у неизвестных поставим индекс i +1, а справа индекс i. В результате получим систему:
3. Осуществим проверку сходимости метода с использованием преобразованной системы (56). Для этого запрограммируем расчет суммы модулей коэффициентов системы уравнений по строкам или столбцам согласно условию (47). Зададим закон изменения среднего времени пребывания t
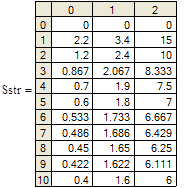
Рассчитаем суммы модулей коэффициентов по строкам системы (56) и поместим результаты в массив Sstr (т. к. имеем три уравнения, то строк три и получаем в массиве Sstr три столбца – 0, 1 и 2, а т. к. t меняется в диапазоне от 1 до 10, а нумерация элементов в массиве начинается с нуля, то получаем в массиве Sstr 11 строк).
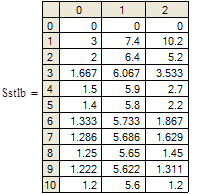
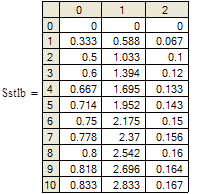
Далее рассчитаем суммы модулей коэффициентов по столбцам системы (56) и поместим результаты в массив Sstlb (т. к. имеем три вещества, то столбцов три и получаем в массиве Sstlb три столбца – 0, 1 и 2, а также 11 строк).
Высветим результаты, анализ которых показывает, что большинство полученных сумм значительно превышает 1 при любом значении t.
Запрограммируем функцию, которая осуществляет проверку условия (47).
Элементы массивов z и u равны 1, если текущее значение в массиве Sstr и Sstlb соответственно меньше 1, иначе элементы массивов z и u равны 0. Элементы массивов р1 и р2 равны 1, если сумма модулей коэффициентов системы (56) по всем строкам или всем столбцам соответственно для каждого t меньше 1. В элементы массива v записывается 1, если условие (47) выполняется. Как видно из результатов, условие (47) не выполняется независимо от того, какое значение принимает t. Это говорит о том, что нами некорректно выбран способ преобразования системы (52) в вид (56). Поэтому попробуем выполнить преобразование по-другому (вариант преобразования 2). Вариант преобразования 2. Используем систему (55)
1. Сгруппируем элементы в уравнениях (55) следующим образом:
а затем
Внимание! Такой вариант является предпочтительным, т. к. значения знаменателей коэффициентов превосходят значения числителей. Именно поэтому во втором уравнении системы (57) для переменной XB множитель k 3 помещен в знаменатель, а k 2 – в числитель (k 3> k 2). При проведении преобразований следует сделать так, чтобы искомая переменная рассчитывалась сама через себя в как можно большем количестве уравнений. Если это не удается сделать для всех уравнений, то хотя бы для одного (любого в системе) уравнения это требование нужно выполнить обязательно. В данном примере это удалось только для второго уравнения системы (57). Здесь концентрация XBi+1 рассчитывается через её же значение на предыдущем шаге XBi, а концентрации веществ XAi+1, XDi+1 рассчитываются через XBi. Такой вариант вполне допустим. 2. Расчет суммы модулей коэффициентов по строкам и столбцам системы (57) дает результаты, которые говорят о том, что большинство полученных сумм не превышает 1 или превышает 1 незначительно. При использовании метода итераций гарантировано получение результата для значений t 1 и 2. Тем не менее, при программировании метода результат получается для всех значений t от 1 до 10.
3. Для метода Зейделя система (57) преобразуется следующим образом:
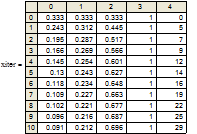
Как видно, во втором уравнении системы для расчета используется значение ХАi+1, полученное на текущей итерации, а в третьем уравнении – ХBi+1. Программирование решения методом итераций и методом Зейделя студент должен осуществить самостоятельно (блок-схемы алгоритмов приведены в пункте 7.4.3 на стр. 127–128). Рекомендации: 1) при программировании использовать вложенные циклы, внешний цикл по t осуществить с помощью оператора for, а внутренний цикл по i – с помощью оператора while, t– среднее время пребывания, i – текущая итерация; 2) для каждого из методов запрограммировать свою функцию расчета; 3) полученные для каждого метода результаты представить в табличном виде и в виде графиков, примерный вид приведен ниже (рис. 46). Пояснение названий массивов: t– среднее время пребывания в реакторе; Xait, Xbit, Xdit – значения концентраций, полученные по методу итераций; Sit –сумма концентраций; Iit – количество итераций, за которое получено решения для каждого t.
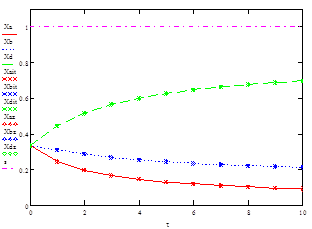
Рис. 46 Результаты решения системы линейных уравнений методом итераций 4) провести сравнительный анализ трех использованных методов (рис. 47)
Рис. 47. Результаты сравнения методов решения системы линейных уравнений
|


 для всех
для всех 
 для всех
для всех  .
.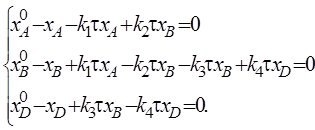 (55)
(55)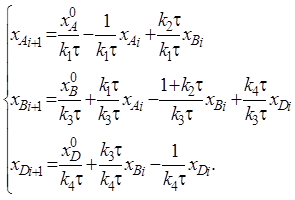 (56)
(56)
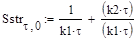
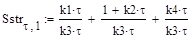
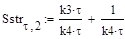
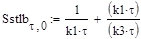
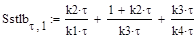
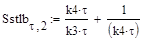



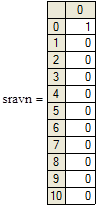
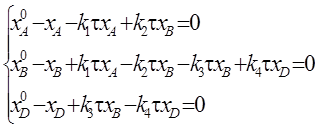

 (57)
(57)

 (58)
(58)