Метод деления отрезка пополам (вилки, дихотомии)
Идея метода состоит в том, что на каждой итерации в качестве очередного приближения к корню выбирается середина отрезка [ a, b ] [ a, x ], если sign (f(x)) ¹ sign (f(а)), т. е. f(x)× f(a) < 0, [ x, b ], если sign (f(x))= sign (f(а)), т. е. f(x) × f(a) > 0.
Рис. 52. Метод дихотомии Таким образом, получается последовательность вложенных отрезков, левые границы которых образуют неубывающую последовательность аk, правая – невозрастающую последовательность bk. При неограниченном увеличении числа итераций k эти последовательности сходятся к общему пределу: последовательность ak слева и последовательность bk – справа. Значение предела является точным значением корня х*. Сужение исходного отрезка до размеров требуемой точности ½ bk – ak ½ £ 2 e позволяет определить приближенное значение корня:
Метод половинного деления требует только информации о значении функции. Для него не нужно условие сходимости, но метод дихотомии относительно медленный, т. е. заданную степень точности можно получить за большее количество итераций, чем при использовании других методов. Блок-схема метода представлена на рис. 53.
|
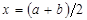(рис. 52), а в качестве нового отрезка для выбора следующего приближения принимается та половина исходного, на концах которого функция f(х) имеет разные знаки:
.
