Метод простых итераций
Для решения методом простых итераций уравнение Стратегия метода заключается в том, что выбирается некоторое начальное приближение х(0) Î [ a, b ] и строится последовательность приближений { x(k) } по рекуррентной формуле:
Рис. 56. Алгоритм поиска корня уравнения методом Ньютона
Рис. 57. Геометрическая интерпретация метода простых итераций При преобразовании уравнения f(x)= 0 к нормальному виду x=j(x) получаем две функции – j(x) и g(x)=x. График g(x) представляет собой прямую, проходящую через начало координат под углом 45°. Вид графика j(x) зависит от того, каким образом было проведено преобразование к нормальному виду. Корень уравнения f(x)= 0 соответствует абсциссе точки пересечения функций j(x) и g(x). Поиск корня осуществляется так. 1. Выбирается начальное приближение x1 (например, точка a – точка 1). 2. На графике j(x) строится точка, соответствующая x1 (точка 2), и рассчитывается значение j(x1) – точка 3. 3. Затем осуществляется переход с кривой j(x) на прямую g(x) (точка 4). 4. Так как у функции g(x)=x значение аргумента совпадает со значением функции, то можно найти значение следующего аргумента x2 (точка 5). 5. Зная x2, можно найти соответствующую точку на кривой j(x) (точка 6), т. е. осуществить переход с прямой g(x) на кривую j(x). 6. Далее повторяются аналогичные действия, заключающиеся в последовательном переходе с кривой j(x) на прямую g(x) и наоборот. При этом рассчитываются значения аргументов и функций в получающихся точках перехода (точки 7–12). 7. Из рис. 57 видно, что этот повторяющийся процесс приведет к получению последовательности приближений к решению { x(k) }, стремящейся к точке пересечения функций j(x) и g(x), т. е. к корню. Для того чтобы получить решение уравнения методом простых итераций, должны выполняться три условия: - каждый член последовательности приближений к решению { x(k) } должен принадлежать отрезку [ a, b ]; - последовательность { x(k) } должна быть сходящейся; - пределом последовательности { x(k) } должно быть значение х*. Для выполнения первого условия достаточно соблюдение неравенства: a£ j(x) £ b " x Î [ a, b ]. Для выполнения второго условия должно соблюдаться следующее неравенство: | x(k+1) – x(k) | < | x(k) – x(k-1) |, но, поскольку x(k+1)=j(x(k)) и x(k)=j(x(k-1)), тогда неравенство будет выглядеть: | j(x(k))– j(x(k-1 ) )| < | x(k) – x(k-1 )| или
В соответствии с теоремой Коши для сходящейся последовательности
Тогда по определению производной:
Получаем достаточное условие сходимости приближений к корню уравнения | j¢ (х) | < 1 " х Î [ a, b ]. (64) Решение уравнения методом простых итераций считается полученным с заданной степенью точности e, когда два последовательных приближения различаются на величину, не превышающую e. | x(k) – x(k+1) | £ e. (65) Преобразование уравнения f(x)= 0 к виду х=j(x) неоднозначно, поэтому для одной и той же функции f(x) могут быть получены различные выражения j(х). При выполнении преобразований следует иметь в виду, что может получиться выражение, не удовлетворяющее условию сходимости (64). В этом случае надо подобрать другое нормальное выражение х=j(x). Рекомендуется уравнение f(x)= 0преобразовать к виду: x=х- m× f(x), т. е. j(х)=х–m× f(x), (66) где m – отличная от нуля константа. Дифференцируя j(х), получим: j¢ (х)= 1- m× f¢ (x). Для того чтобы выполнялось условие (64) ½ j¢ (х) ½ = ½ 1 -m× f¢ (x) ½ £ 1, достаточно подобрать m так, чтобы для " х Î [a, b] выполнялось неравенство: 0< m× f¢ (x) < 2. (67) Пример. Требуется уточнить корень уравнения sin ( 2 x)- ln (x) =0 на интервале [ a, b ]. Тогда f(x)= sin ( 2 x) - ln (x). Представим это уравнение в виде: x=x- m× ( sin ( 2 x) - ln (x). В этом случае j (x)=x - m× ( sin ( 2 x) - ln (x)), j¢ (x)= 1 - m× ( 2cos ( 2 x) - 1 /x). Подберем константу m так, чтобы выполнялось условие 0< m× f¢ (x) < 2. Для этого на интервале [a; b] (рис. 58) постоим функцию f¢ (x) = 2cos ( 2 x) - 1 /x.
Рис. 58. График функции f¢ (x) = 2cos ( 2 x) - 1 /x По приведенному графику получаем значение М = f¢ (1, 5)= - 2, 647, определяющее максимальное значение функции f¢ (x) на интервале [ a; b ]. Если принять значение константы m=- 1 /М, то для всех х Î [1; 1, 5] функция mf¢ (x) удовлетворяет условию (67) (рис. 59).
Рис. 59. График функции mf¢ (x) = m (2cos(2 x) - 1/ x) Таким образом, мы добились того, чтобы выполнялось условие сходимости (64) (рис. 60).
Рис. 60. График функции j¢ (x)= 1 -m× ( 2cos ( 2 x) - 1 /x) В результате будем искать с помощью метода итераций точку пересечения функций j(x)=x-m× ( sin ( 2 x) - ln (x)) и g(x) = х (рис. 61).
Рис. 61. Поиск корня методом итераций по функциям j(x) и g (х)
После подбора выражения j(x) можно приступить к реализации алгоритма поиска корня (рис. 62).
|

 надо привести к нормальному виду
надо привести к нормальному виду  , т. е. графически решением уравнения, является точка х=х* (рис. 57), в которой совпадают значения абсциссы и ординаты функции j (x).
, т. е. графически решением уравнения, является точка х=х* (рис. 57), в которой совпадают значения абсциссы и ординаты функции j (x). , k= 1, 2, …
, k= 1, 2, …
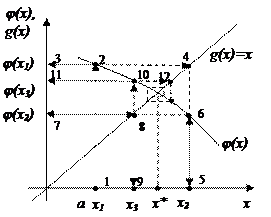
 .
. .
. .
.








