Метод Ньютона. Рассмотрим систему нелинейных уравнений 2-го порядка (89) в общем виде
Рассмотрим систему нелинейных уравнений 2-го порядка (89) в общем виде. Однако необходимо учитывать, что метод Ньютона может использоваться и для систем уравнений более высокого порядка.
Выберем х0 и у0 в качестве грубого приближения к решению, х0 и у0 могут выбираться либо на этапе отделения корней, либо из физических соображений или при постановке задачи.
Рис. 79. Отделение корней Для реализации последовательного приближения грубого приближения к решению (точному) х и у необходимо записать в алгоритм поиска наиболее точного решения в следующем виде:
где i =0, 1, ¼, при условии, что х0 и у0 известны. То есть для решения системы уравнений необходимо указать правила нахождения добавок hi, ki. Для этого введем следующее обозначение
Подставим (93) в систему (89):
Разложим уравнения системы (94) в ряд Тейлора в окрестностях точки (х0, у0), при этом ограничимся линейными членами разложения:
где q1, q2 – нелинейные относительно (x-x0) и (y-y0) члены разложения.
Если пренебречь q1 и q2, обозначить то получим систему линейных уравнений относительно h и k:
Решение системы (96) даст неизвестные h и k, которые приближают х0, y0 к точному решению, но точного значения корня не обеспечивают (вследствие пренебрежения остаточными членами разложения q1 и q2). Т. к. f(x0, y0), j(x0, y0), f’x(x0, y0), f’y(x0, y0), jx’(x0, y0), jy’(x0, y0) – константы, то систему уравнений (96) можно представить в привычном виде:
Решение системы (97) может быть получено с использованием методов решения систем линейных уравнений, например, правила Крамера:
Определитель матрицы, составленный из первых производных системы уравнений, называется Якобианом. После того как h и k найдено, необходимо повторять процесс поиска новых значений h и k и до тех пор, пока решение не достигнет заданной степени точности e. При этом в качестве начального приближения выбирается всякий раз очередное приближение к решению, т. е. итерационный процесс поиска можно представить в следующем виде:
Условием прекращения поиска решения является выполнение следующего условия:
причем эти условия должны выполняться одновременно. Таким образом, поиск решения выполняется при реализации следующей последовательности действий: 1) выбираются начальные значения х0 и у0; 2) для этих значений рассчитываются значения функций f, j, f'x, f'y, j’x, j’y; 3) решается система линейных уравнений (96), т. е. находятся значения h и k; 4) по формулам уравнений (98) находятся значения х, у. Процесс поиска, т. е. действия (2)–(4) выполняются до тех пор, пока не выполнится условие достижения заданной степени точности (99). Блок-схема решения системы нелинейных уравнений методом Ньютона представлена на рис. 80.
|



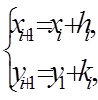 (92)
(92) . (93)
. (93) . (94)
. (94) , (95)
, (95)

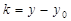 ,
, 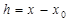 ,
, . (96)
. (96)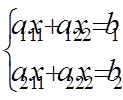 . (97)
. (97) ;
;  , где
, где 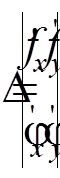


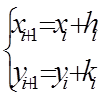 . (98)
. (98) , (99)
, (99)


