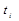Постановка задачи. 1. В соответствии с выбранным вариантом (пункт 10.7, табл
1. В соответствии с выбранным вариантом (пункт 10.7, табл. 9) осуществить решение обыкновенного дифференциального уравнения 1-го порядка 2. Произвести оценку погрешностей метода Эйлера, модифицированного метода Эйлера, метода Эйлера-Коши, рассчитанных относительно решения, полученного методом Рунге-Кутта 4-го порядка по следующей формуле (%):
где N – число точек решения; 3. Дать сравнительную характеристику методов, используемых для решения дифференциального уравнения по следующим характеристикам:
- сложность реализации метода (преимущества и недостатки); - точность метода. 4. Результаты представить в виде графиков и в табличном виде.
|
на интервале 
с начальным условием x(t0)=x0 и временем дискретизации Δ t четырьмя методами: методом Эйлера, модифицированным методом Эйлера, методом Эйлера-Коши, методом Рунге-Кутта 4-го порядка.
,
и 
– решение, полученное по выбранному методу и по методу Рунге-Кутта 4-го порядка на i -м шаге итераций; 
и 
– максимальные и минимальные значения, полученные по методу Рунге-Кутта 4-го порядка.
