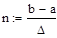Решение обыкновенного дифференциального уравнения 1-го порядка с помощью функции rkfixed

Пусть имеется уравнение вида: .

Необходимо найти его решение на интервале [a, b] при начальном условии x(0)=x0.

В математическом редакторе Mathcad существует встроенная функция rkfixed, которая сама осуществляет решение методом Рунге-Кутта 4-го порядка. Использовать её необходимо следующим образом.

Сначала задаются параметры, которые будут передаваться в указанную функцию:

x0 – вектор начальных условий, в данном случае вектор из одного элемента;

a, b – границы интервала для поиска решения;

n– количество точек на интервале;

D(t, x) – вектор-функция первых производных, в данном случае вектор из одного элемента.

Вызов функции осуществляется так:

rkfixed(x0, a, b, n, D)

 

Запрограммируем процесс решения.

1. Задаем начальное условие:

2. Вводим правую часть дифференциального уравнения:

В данном случае элемент x₀ набирается с использованием кнопки Matrix®Subscript (Матрицы®Нижний индекс) или горячие клавиши Shift+] (или Shift+ъ при русской раскладке клавиатуры)

3. Задаем интервал поиска решения:

4. Задаем шаг дискретизации:

5. Задаем число точек дискретизации:

6. Осуществляем вызов функции и высвечивем результаты:

Матрица Z имеет 2 столбца и 40 строк. Первый столбец содержит переменную t, второй – переменную x. Решение дифференциального уравнения представлено на рис. 89.

Рис. 89. Решение уравнения на интервале [1, 5].