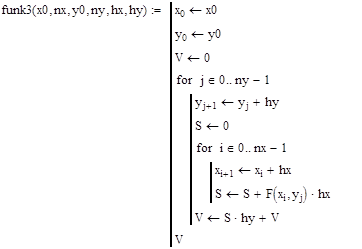Пример выполнения
Рассмотрим процесс расчета двойного интеграла методом левых прямоугольников по внешнему и внутреннему контуру.
Расчет проведем в среде Mathcad. 1. Сначала зададим вид функции двух переменных:
2. С помощью символьных вычислений получим аналитическое значение неопределенного интеграла нашей функции:
3. Зададим пределы интегрирования по внутреннему и внешнему контуру:
4. Рассчитаем с помощью Mathcad значение определенного интеграла (точное). С этой величиной сравним результат, полученный численным методом.
5. Зададим шаг разбиения интервалов интегрирования по внутреннему и внешнему контурам:
6. Используя заданные значения шагов, рассчитаем число точек, на которое разбиваются интервалы:
7. Используя инструменты программирования Mathcad, составим подпрограмму расчета двойного интеграла согласно методу левых прямоугольников.
Расчет проводится путем организации вложенных циклов. Внутренний цикл (по параметру i) предназначен для расчета площади под кривой, ограниченной функцией F(x, y), а также прямыми x=a и x=b при фиксированном значении y. Внешний цикл (по параметру j) предназначен для расчета объема под криволинейной поверхностью, ограниченной функцией F(x, y), а также четырьмя плоскостями, образуемыми пределами интегрирования (a, b, c, d). 8. Рассчитаем интеграл. Для этого осуществим вызов функции расчета интеграла с передачей в нее заданных параметров:
9. Сравним полученный результат с результатом, полученным в пункте 4 (они должны быть приблизительно равны). 10. С помощью Mathcad строим график «Столбиковая диаграмма», отражающий вид функции F(x, y), используемой для расчета интеграла (рис. 97). С помощью опции QuickPlotData, вызываемой двойным нажатием мыши на построенной диаграмме, устанавливаем диапазоны интегрирования (Range1 и Range2), определяемые численными значениями a, b, c, d.
Рис. 97. Диаграмма, отражающая функцию F(x, y) в заданных пределах интегрирования
|

 .
. .
.