Метод прямоугольников
Пусть функция f(x) задана таблично, необходимо найти  График функции f(x) можно представить на плоскости f(x) и x (рис. 91).
Рис. 91. График функции f(x) Условия интерполирования обозначим следующим образом:
где n – число интервалов разбиения. Каждому узлу интерполирования в соответствии с табличным заданием функции f(x) поставлено в соответствие следующее значение: y0 = f(x0) ¼ (121) yn = f(xn) Определенный интеграл представляет собой сумму площадей под кривой f(x) на каждом шаге интерполирования:
Площадь Si можно приблизительно определить как площадь прямоугольника, образованного координатой f(xi) и шагом интерполирования h. S1»f(x0)× h S2»f(x1)× h ¼ (123) Sn»f(xn)× h. В результате общая площадь S определяется как сумма всех площадей, т. е.
Формула (124) - формула левых прямоугольников. Существует еще и формула правых прямоугольников:
Уменьшение шага интерполирования h ведет к возрастанию точности интегрирования методом прямоугольников.
|
. (120)
. (122)
(124)
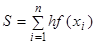. (125)
