Метод Эйлера-Коши
Необходимо решить уравнение (101): Если предположить, что функция x(t) проходит черезпромежуточную точку (xi*, ti+1), то в ней также можно построить касательную II к функции x(t). Касательная II пройдет под углом b. Проведем через точку (xi*, ti+1) прямую III под углом g так, чтобы выполнялось равенство:
Через точку (xi, ti) проведем прямую IV параллельно прямой III. Она тоже пройдет под углом g. Точка пересечения прямой IV с вертикалью ti+1 представляет собой следующую искомую точку (xi+1, ti+1) функции x(t). Осуществим вывод формулы для расчета функции x(t). Согласно рис. 88:
где xi, xi+1 – текущая и последующая точки функции x(t) соответственно; Δ x – приращение функции x(t) на интервале Δ t.
Величину Δ x найдем из прямоугольного треугольника с углом g:
При малых отклонениях углов a и b можно воспользоваться формулой:
Согласно геометрическому смыслу первой производной функции:
Согласно рис. 88:
Величину Δ x* найдем из прямоугольного треугольника с углом a:
Подставив все полученные значения в исходную формулу, получим формулу метода Эйлера-Коши:
Пример. Для уравнения
|
. Проведем в точке 
касательную I к функции x(t) (рис. 88). Она пройдет под углом a. Пересечение касательной I с вертикалью ti+1 назовем промежуточной точкой xi*.
.
,
. (113)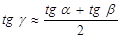
. (114)
,
. (115)
, 
.
. (116)
. (117)
запишем формулу расчета функции x(t) согласно методу Эйлера-Коши
