Расчет двойного определенного интеграла

Пусть имеется функция двух переменных f(x, y). Необходимо вычислить определенный интеграл

.

В этом случае геометрическая интерпретация определенного интеграла такова – если f(x, y)³ 0 при x Î [ a, b ] и y Î [ c, d ], то интеграл представляет собой объем области, ограниченной плоскостями xoy, x=а, x=b, y=c, y=d и графиком f(x, y) (рис. 96).

Разобьём интервал [ a, b ] на конечное число участков с шагом hx, а интервал [ c, d ] – с шагом hy. Если зафиксировать y = c, то получим плоскую фигуру, как на рис. 90. Её площадь S 1 можно рассчитать как сумму элементарных площадей по рассмотренным выше методам, например, по методу трапеций. Если умножить полученную площадь на величину hy, то получим элементарный объём V 1. Затем фиксируем y = c + hy, т. е. берем следующее сечение. Рассчитываем площадь полученной фигуры S 2 опять по методу трапеций. Эта площадь будет отличаться от предыдущей, т. к. функция f(x, y) чаще всего нелинейна. Также умножаем значение площади на величину hy, т. е. получаем второй элементарный объем V 2, и суммируем его с предыдущим. Повторяем описанные действия, пока не пройдем весь интервал [ c, d ]. В результате получим объем, численное значение которого соответствует величине искомого определенного двойного интеграла.

В данном случае внутренний контур (по переменной x) рассчитывался методом трапеций, а внешний (по переменной y) – методом левых прямоугольников.

Для расчета внутреннего и внешнего контуров можно использовать любой из рассмотренных выше методов. При этом нужно помнить, что при расчете внутреннего контура вычисляется площадь, для чего используются значения функции f(x, y) при фиксированном y. При расчете внешнего контура вычисляется объем, для чего используются значения площадей, полученные во внутреннем контуре.

Например, если для расчета внешнего контура использовать метод трапеций, то первый элементарный объем V 1 вычисляется согласно формуле (126) так:

Рис. 96. Геометрическая интерпретация определенного

двойного интеграла
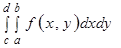