Численное решение систем дифференциальных уравнений
Пусть имеется система обыкновенных дифференциальных уравнений 1-го порядка, записанная в нормальной форме Коши:
с начальными условиями Численная схема решения системы уравнений (136) согласно методу Эйлера будет выглядеть:
где Dt – интервал дискретизации; Численная схема решения системы уравнений (136) согласно модифицированному методу Эйлера будет выглядеть:
где xi*, yi*, ti* – промежуточные точки, рассчитываемые следующим образом:
Если подставить значения промежуточных точек в формулы (138), получим:
Численная схема решения системы уравнений (136) согласно методу Эйлера-Коши будет выглядеть:
где xi*, yi*, ti* – промежуточные точки, рассчитываемые следующим образом:
Если подставить значения промежуточных точек в формулы (140), получим:
Численная схема решения системы уравнений (136) согласно методу Рунге-Кутта 4-го порядка будет выглядеть:
где X 1 i, X 2 i, X 3 i, X 4 i, Y 1 i, Y 2 i, Y 3 i, Y 4 i – промежуточные точки, рассчитываемые следующим образом:
Пример. Имеется система нелинейных дифференциальных уравнений:
Задача: составить численные схемы решения системы уравнений (143). Метод Эйлера.
Модифицированный метод Эйлера.
или
Метод Эйлера-Коши.
или
Метод Рунге-Кутта 4-го порядка.
|

 (136)
(136) ,
,  .
.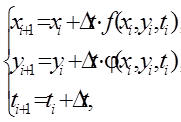 (137)
(137) – номер интервала;
– номер интервала;  – количество интервалов; с начальными условиями
– количество интервалов; с начальными условиями 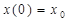 ,
,  .
. (138)
(138) ,
, ,
,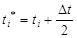 .
. (139)
(139) (140)
(140)
 ,
, .
. (141)
(141) (142)
(142)





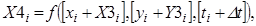

 (143)
(143) (144)
(144) (145)
(145) (146)
(146)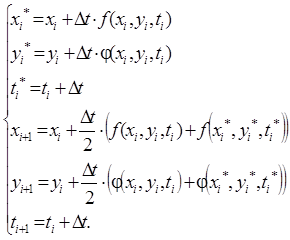 (147)
(147) (148)
(148) (149)
(149)



