Вывод уравнения диффузии для неподвижной среды
Рассмотрим процесс диффузии вещества из раствора с концентрацией С 0=const в растворитель (концентрация данного вещества в начальный момент времени равна нулю), ограниченный проницаемыми пластинами (рис. 101). Изучим процесс диффузии вещества в растворителе. Перенос вещества происходит благодаря молекулярной диффузии (т. к. среда неподвижна) за счет разницы концентраций в растворе и растворителе.
Рис. 101. Процесс диффузии вещества Опытным путем установлено, что скорость распространения вещества j, т. е. количество вещества, проходящего через сечение с абсциссой х за единицу времени, определяется формулой:
где f – площадь поверхности рассматриваемого сечения, м2; D – коэффициент диффузии, м2/ч, С – концентрация вещества, моль/м3. Рассмотрим элемент объема (рис. 102), заключенного между сечениями х1 и х2 (х2-х1=Dх).
Рис. 102. Процесс диффузии в элементе объема Количество вещества, проходящего через сечение с абсциссой х1 за время Dt, будет равно:
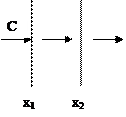
То же самое для сечения х2:
Приток вещества
За счет притока вещества в элементарном объеме (f.Dх) произошло изменение концентрации на величину Dс, т. е. мы можем записать материальный баланс для элементарного объема:
Разделим левую и правую часть уравнения на f.Dх.Dt и учитывая, что
т. е. мы получили уравнение, описывающее перенос массы в неподвижной среде в направлении х. Его необходимо дополнить начальными и граничными условиями. Начальные и граничные условия полученного уравнения, исходя из постановки задачи, могут быть заданы следующим образом:
Если бы в задаче было сказано, что одна пластина непроницаема для вещества (правая пластина на рис. 101), то начальные и граничные условия должны быть заданы следующим образом:
Условие
|


 ,
,
 .
.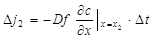 .
.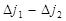 в элементарном объеме за время Dt будет равен:
в элементарном объеме за время Dt будет равен: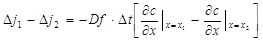 .
.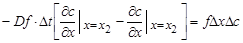
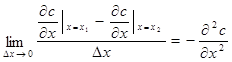 ,
, 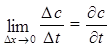 , получим
, получим , (158)
, (158)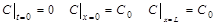 .
.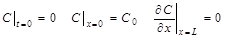
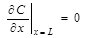 означает, что скорость изменения концентрации по координате на границе равна 0.
означает, что скорость изменения концентрации по координате на границе равна 0.


