Пример выполнения. Пусть в изотермическом реакторе идеального вытеснения протекает реакция типа:
Пусть в изотермическом реакторе идеального вытеснения протекает реакция типа:
Численное интегрирование осуществим методом Эйлера при следующих начальных условиях:
U =1 м/с, l =2 м, Dl = 0, 1 м. Реактор идеального вытеснения представляет собой аппарат с непрерывной подачей реагентов, в котором они перемещаются с постоянной скоростью в поршневом потоке. Математическое описание реакторов этого типа в стационарных изотермических условиях можно получить, исходя из системы уравнений, определяющей изменение концентраций реагентов в зоне идеального вытеснения с учетом скорости их образования:
где XA, XP, XD – концентрации реагентов (исходных продуктов или продуктов, образующихся в зоне реактора); wA, wP, wD – скорости образования (исчерпывания) веществ, с-1; l – линейная координата, м; U – линейная скорость подачи веществ в зону реакции, м/с. Для реакции, приведенной в задании, можно выделить следующие элементарные стадии:
Тогда скорости образования всех участвующих в сложной химической реакции реагентов можно представить в виде:
где Модель реактора идеального вытеснения (150) с учетом (151) описывается системой дифференциальных уравнений:
Начальные условия: Проведем аппроксимацию полученной системы дифференциальных уравнений конечно-разностными уравнениями на интервале l Î [0, L ] с шагом Dl в соответствии с рассмотренными выше методами. Полученная система конечно-разностных уравнений позволит осуществить расчет профиля концентраций по длине реактора (рис. 99). Численная схема, полученная согласно методу Эйлера:
где Численная схема, полученная согласно модифицированному методу Эйлера:
или
Численная схема, полученная согласно модифицированному методу Эйлера-Коши:
или
Численная схема, полученная согласно методу Рунге-Кутта 4-го порядка:
Рис. 99. Блок-схема алгоритма расчета профиля концентраций
|
.
,
,
,
(150)
; 
.
,
, (151)
,
; 
.
(152)
, 
, 
.
(153)
, 
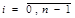, с начальными условиями 
, 
, 
.
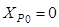(154)
(155)
(156)
