Условия устойчивости явной разностной схемы
Для того чтобы решение по явной разностной схеме было устойчиво, необходимо выбирать интервалы дискретизации из следующего условия:
Конечно-разностная схема называется устойчивой, если погрешности, допущенные в процессе вычислений, затухают или остаются малыми при увеличении номера текущего слоя. Рассмотрим условия устойчивости явной разностной системы на примере уравнения диффузии:
Будем искать решение в следующем виде.
где А – const, f = – w 2, Отметим, что eiwx =cos(wx)+i× sin(wx), т. е. физически решением уравнения являются функции, которые представляют собой волны, графиком которых являются кривые (гармоники), затухающие при t ®¥. Рассмотрим конечно-разностные уравнения, аппроксимирующие исходное дифференциальное уравнение.
Очевидно, что затухание гармоник во времени должно иметь место и для разностного уравнения. Решение данного уравнения будем искать в виде:
где: tn =(n -1)D t, xk =(k -1)D x. Если положить
Следовательно, при
Разделим левую и правую части уравнения на: G = AS n-1 e iw(k-1)Dx, получим:
Рассмотрим
следовательно,
Для устойчивости вычислительной схемы достаточно потребовать, чтобы ê S ê £ 1, т. е.
Правое неравенство выполняется всегда.
Рассмотрим случай, когда sin принимает максимально возможное значение – 1:
Для получения устойчивого решения уравнения, сначала задаются одним из параметров (например, величиной Dх) и затем, исходя из полученного условия определяется величина другого значения Dt.
|
.
.
.
.
,
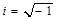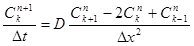, то 
.
происходит затухание гармоники во времени, т. е. процесс решения устойчив. Если ê S ê > 1, то происходит потеря устойчивости решения. Для конечно-разностного уравнения, подставив формулу предполагаемого решения, получим:
.
,
.
.
