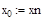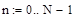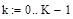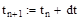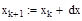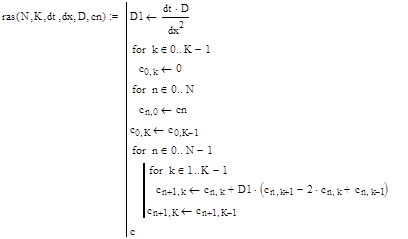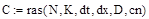Пример выполнения. Рассмотрим процесс расчета профиля концентрации вещества по пространственной и временной координате для объекта
Рассмотрим процесс расчета профиля концентрации вещества по пространственной и временной координате для объекта, описываемого следующим уравнением:
где С – концентрация вещества; D – коэффициент диффузии; t – время; x – пространственная координата. Начальные условия:
Граничные условия:
Расчет проведем в среде Mathcad. 1. Сначала зададим исходные данные для расчета:
2. Выбираем шаг дискретизации по времени так, чтобы выполнялось условие устойчивости явной разностной схемы:
3. Рассчитываем количество точек разбиения временного и пространственного интервалов для метода сетки:
4. Рассчитаем массивы временного и пространственного интервалов (индекс k – порядковый номер элементов в массиве пространственной координаты, индекс n – порядковый номер элементов в массиве времени):
5. Используя инструменты программирования Mathcad, составим функцию, реализующую расчет профиля концентраций по явной разностной схеме:
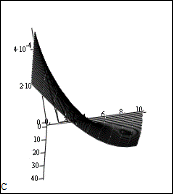
6. Осуществим вызов данной функции и возврат её результатов в массив C: 7. Выведем на экран содержимое массивов x, t и C. Для этого после имени массива поставим знак «=». 8. Представим полученную зависимость концентрации от времени и длины в виде объемного графика (рис. 105):
Рис. 105. Изменение концентрации по времени и длине 9. Представим распределение концентрации в конкретных сечениях (длина фиксирована) по времени (рис. 106):
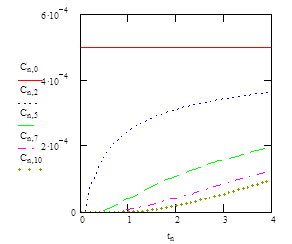
Рис. 106. Изменение концентрации по времени 10. Представим распределение концентрации в конкретные моменты времени в сечениях (время фиксировано) по длине (рис. 107):
Рис. 107. Изменение концентрации по длине 11. Проведем анализ полученных результатов с точки зрения физического смысла. Рассмотрим процесс изменения концентрации во времени в нескольких выбранных сечениях: - на одной границе (x =0) концентрация постоянна, что соответствует первому граничному условию; - на другой границе (x = L) градиент концентраций отсутствует, т. к. значения рассчитанных концентраций в двух последних сечениях (при x = L и x = L – dx) равны, что соответствует второму граничному условию; - во всех сечениях происходит увеличение концентрации со временем (рис. 106), т. к. происходит поступление вещества внутрь объекта через его границу благодаря диффузии, причем в сечениях, близких к границе x = L, концентрация увеличивается значительно позже, чем в сечениях, близких к границе x =0. Рассмотрим процесс изменения концентрации по длине в определенные моменты времени: - в начальный момент времени (t =0) концентрация в объекте равна нулю во всех сечениях, за исключением границы x =0, что соответствует начальному условию; - в любой из рассматриваемых моментов времени (рис. 107) концентрация на границе x =0 превышает концентрацию на границе x = L, но чем больше проходит времени, тем меньше становится разница концентраций, что говорит о постепенном проникновении вещества внутрь объекта. Таким образом, проведенный анализ результатов, представленных в виде таблиц и графиков, показывает, что результаты соответствуют физическому смыслу задачи.
|

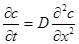 ,
,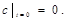
 ,
, 
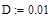 –коэффициент диффузии,
–коэффициент диффузии,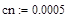 – начальная концентрация,
– начальная концентрация,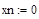 – начальное значение пространственной координаты,
– начальное значение пространственной координаты,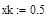 – конечное значение пространственной координаты,
– конечное значение пространственной координаты,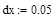 – шаг дискретизации по пространственной координате.
– шаг дискретизации по пространственной координате.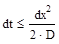

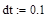 – шаг дискретизации по времени,
– шаг дискретизации по времени,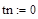 – начальное время,
– начальное время,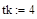 – конечное время,
– конечное время,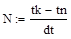 ,
,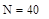 – для временного интервала,
– для временного интервала,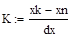 ,
,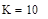 – для пространственного интервала.
– для пространственного интервала.