Задания. Задачи, описываемые уравнением вида
Задачи, описываемые уравнением вида
Вариант 1. Растворенное вещество с начальной концентрацией с 0(0, 5 моль/дм3) диффундирует из раствора, заключенного между плоскостями х=0 и х=h. Определить процесс выравнивания концентраций, предполагая, что границы х=0 и х=l непроницаемы для вещества. Расстояние между h и l принять равным единице. Коэффициент диффузии взять равным 10-3см2/с. Конечное время процесса tk = 20c. Начальные и граничные условия примут вид:
Вариант 2. Сосуд высотой h = 1 см заполнен раствором соли, концентрация которой 100 моль /дм3. Он погружен в емкость с большим количеством воды так, что открытый край сосуда находится непосредственно под поверхностью воды и находится с нею в соприкосновении. Граничные условия:
Найти распределение концентрации соли в любой момент времени (tk = 5 с; D = 10-2 см2/с). Вариант 3. Плоская керамическая плита толщиной 4 см подвергается сушке с двух сторон. Начальное содержание влаги с = 0, 5 г/см3. Распределение внутри массы происходит за счет молекулярной диффузии (D = 0, 25 см2/ч). Известно, что при данных условиях сушки процесс протекает за период постоянной скорости сушки со скоростью 0, 1 г/(ч•см2) воды до тех пор, пока поверхностное содержание влаги остается выше 0, 22 г/см3. Установить продолжительность периода постоянной скорости сушки, количество испарившейся влаги и распределение влаги внутри пластины к концу периода постоянной сушки. Площадь поверхности плиты 1 м2. tk = 15 ч; Граничные условия:
Задачи, описываемые уравнением вида
Вариант 4. Дан тонкий однородный стержень длиной 50 см, начальная температура которого равна нулю. На конце х=l температура поддерживается равной нулю, а ни конце х= 0 она растет линейно от времени по закону Т(t, 0 ) = a·t (а = 20). Найти распределение температуры вдоль стержня в любой момент времени. Конечное время tk =10 с. Коэффициент температуропроводности α 2 взять равным 0, 1 м2/с. Вариант 5. Условие такое же, как в варианте 4, нограничное условие конце х= 0 имеет вид: T (t, 0) = Вариант 6. Дана бесконечная пластина стали толщиной 0, 3 м, имеющая начальную температуру 700 °С. Наружные плоскости её мгновенно охлаждаются и их температура поддерживается равной 100 °С. Требуется определить значение температуры в среднем сечении, параллельном наружным плоскостям, по истечении 15 мин. Плотность стали γ = 7800 кг / м3; удельная теплоемкость стали с = 460 Дж/(кг•°С); коэффициент теплопроводности λ = 45, 4 Вт/(м•°С). Коэффициент температуропроводности α 2 определяется как Вариант 7. Дан тонкий однородный стержень длиной 1 м, боковая поверхность которого теплоизолирована. Начальная температура стержня 100 °С. Конец стержня х= 0поддерживается при температуре, равной нулю, а на конце х=l происходит теплообмен с окружающей средой, температура которой считается равной нулю. Определить распределение температуры вдоль стержня в любой момент времени. Граничные условия на одном конце Вариант 8. Решить задачу 7, предполагая, что теплообмен с окружающей средой происходит на обоих концах. Вариант 9. Получить численное решение уравнения
с начальным условием
А =5, 0; a =1; H =0, 35; tk =30 с; a2 =0, 064 м2/мин; L =1 м. Вариант 10. Решить задачу об остывании однородного стержня с теплоизолированной боковой поверхностью, если его начальная температура T ½ t =0 = 1500 °С, один конец теплоизолирован, а другой поддерживается при постоянной температуре T0 =0 °С. tk =1 ч; a2 =0, 036 м2/ч; L =1 м. Граничные условия: Задачи, описываемые уравнениями вида
Вариант 11. Растворимый газ взаимодействует с жидкостью или с растворенным в ней веществом. Скорость расходования газа определяется реакцией первого порядка k·CA. Уравнение, описывающее процесс растворения газа, имеет вид:
Константа скорости химической реакции k = 0, 1 с-1; tk = 20 с; D = 10-2 см2/с. Определить профиль концентраций в жидкой фазе в любой момент времени. Толщина пленки жидкости 1 см. (СA0 = 0, 5 моль/дмЗ). Задачи, описываемые уравнениями вида
Если λ =2, имеем шар, если λ =1, имеем цилиндр. Вариант 12. Дан однородный шар радиуса R =5 см при температуре, равной нулю. Шар нагревается равномерно по всей поверхности постоянным тепловым потоком q = 500 ккал/(м2× ч) (1 кал=4, 187 Дж). Найти распределение температуры по радиусу шара в любой момент времени. Начальные и граничные условия:
(k = 0, 91 Вт/(м2·°С); a 2 = 0, 04 м2/ч; tк = 2 мин). Вариант 13. Диффузионной средой является цилиндр радиуса R =10 см, на поверхности которого постоянная концентрация с 0=0, 1 моль/дм3. Вначале среда свободна от растворенного вещества. Найти распределение концентрации вещества по радиусу цилиндра в любой момент времени (D = 0, l см2/с; tk = 10 с). Начальные и граничные условия:
Вариант14. Однородный шар радиуса R =50 см находится при постоянной температуре Т 0=300°С и окружен сферической оболочкой из того же материала толщиной R, находящейся при температуре, равной 0 °С. Все это охлаждается в среде с температурой, равной нулю. Найти температуру в точках внутри шара на расстоянии r от центра в любой момент времени (α 2 = 0, 01 м2/ч; tк = 0, 5 ч). Граничные условия для центра шара:
Вариант 15. Сфера радиуса R = 2 см содержит растворенное вещество с начальной концентрацией С0 = 0, 1 моль/дмЗ. Концентрация на поверхности сферы поддерживается постоянной и равной 1 моль/дм3. Найти количество абсорбированного вещества в шаре через 10 мин. (D = 10-2 см2/с). Граничные условия в центре шара: Вариант 16. Найти распределение температуры внутри бесконечного кругового цилиндра радиуса R = 5 cм при условии, что начальная температура равна Граничное условие для центра цилиндра: Вариант17. Дан однородный шар радиуса R =20 см. Известна начальная температура шара T0 =100 °С. Внешняя поверхность шара поддерживается при нулевой температуре. Найти распределение температуры по радиусу шара в любой момент времени (а 2=0, 1 м2/ч; tk = 3 мин). Граничное условие в центре шара:
|

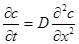


 = 0, 5 г/см3.
= 0, 5 г/см3. .
.
 (w = 0, 5).
(w = 0, 5). .
. , а на конце где происходит теплообмен
, а на конце где происходит теплообмен 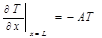 , А =1, 9. Коэффициент температуропроводности α 2 принять равным 1, 9× 10-2 м2/с, а конечное время 6 с.
, А =1, 9. Коэффициент температуропроводности α 2 принять равным 1, 9× 10-2 м2/с, а конечное время 6 с.
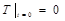 и граничными условиями:
и граничными условиями:


 .
.
 или
или  .
.
 .
. .
. .
. , при Т0= 50 °С, а на боковой поверхности температура поддерживается равной нулю (а 2= 0, 1 см2/с; tk = 50 с).
, при Т0= 50 °С, а на боковой поверхности температура поддерживается равной нулю (а 2= 0, 1 см2/с; tk = 50 с). .
.


