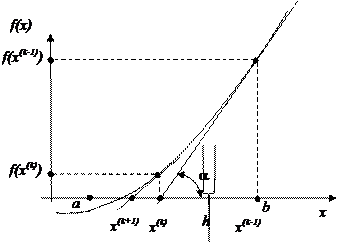Метод Ньютона (метод касательных)
Общая стратегия метода состоит в замене на каждой итерации функции f(x) приближенной линейной зависимостью. Замена функции прямой, т. е. её линеаризация, проводится следующим образом. Пусть имеется такое приближение х(k-1) к корню уравнения, что оно отличается от точного решения на достаточно малую величину h(k): x*=x(k-1) + h(k) , тогда функция f(x) в окрестности точки х(k-1) может быть разложена в ряд Тейлора
Т. к. f(x*) º 0, то, ограничиваясь линейными относительно h членами разложения, можно получить формулу для приближенного расчета шага h(k):
Значение h(k) не точно. Тем не менее, оно дает новое приближение х(k)=x(k-1) + h(k), (62) которое расположено ближе к корню, чем предыдущее. Тогда из новой точки x(k) можно сделать еще один шаг для дальнейшего уточнения значения корня по той же методике. В результате организуется итерационный алгоритм поиска корня уравнения из выбранной некоторым образом точки начального приближения х(0).
Рис. 53. Алгоритм поиска корня уравнения методом дихотомии Вычисления заканчиваются тогда, когда два последовательных приближения различаются на величину, не превышающую заданной точности e, т. е.
В геометрической интерпретации производная определяет тангенс угла a наклона касательной к функции (рис. 54). Поэтому значение h(k) (61) можно также получить из прямоугольного треугольника, образующегося с помощью касательной.
Рис. 54. Геометрическая интерпретация метода Ньютона Как видно из приведенного рисунка, очередным приближением к решению оказывается точка пересечения оси х с касательной, проведенной к графику функции в точке с координатами (х(k-1)), f(x(k-1)). Однако если касательные проводить из точки a, то уточнение корня не будет происходить. Рассмотрим другой возможный график функции (рис. 55). В этом случае проводить касательные нужно из точки a. Из приведенных рисунков видно, что для уточнения корня функции f(x) на [a, b] нужно определить, с какого конца интервала необходимо начинать итерационный процесс поиска. Если f’(x)* f² (x) > 0или f(b)* f² (x) > 0, где " x Î [ a, b ], то процесс поиска начинается с точки b. Если f’(x)* f² (x) < 0 " x или f(а)* f² (x) > 0, то процесс поиска начинается с точки а.
Рис. 55. Возможное поведение функции Метод Ньютона требует информации о значении функции, ее первой и второй производной, т. е. большей, чем метод дихотомии. Но метод Ньютона теоретически обладает самой высокой скоростью сходимости. Кроме того, метод Ньютона не требует выполнения каких-либо условий сходимости последовательности xk. Блок-схема реализации метода приведена на рис. 56.
|


 . (61)
. (61)
 или
или 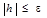 . (63)
. (63)