Пример выполнения задания методом итераций
1. Задаем ранжированную переменную
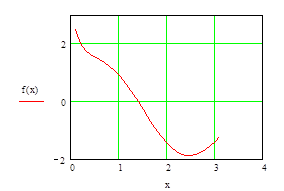
2. Задаем вид функции f(x), строим её график (рис. 63)
Рис. 63. График функции f(x) 3. По рис. 63 проводим отделение корней.
В результате график выглядит так (рис. 64):
Рис. 64. График функции f(x) на интервале [ a, b ] 4. Задаем вид функции j(x) и получаем её вид, а также вид её производной в символьном виде
5. Задаем значение константы m сначала равным единице:
6. Строим график функции j¢ (x) (рис. 65)
Рис. 65. График функции j¢ (x) на интервале [ a, b ] при m =1 7. Как видно, значения графика превышают единицу, т. е. условие (64) не выполняется. Поэтому подберем значение коэффициента m. Для этого строим график функции f¢ (x) (рис. 66).
Рис. 66. График функции f¢ (x) на интервале [ a, b ] 8. По графику получаем значение М = f¢ (1, 5)»-2, 75, определяющее максимальное значение функции f¢ (x) на интервале [ a; b ]. Для более точного определения значения M задаем функцию
и находим значение этой функции на конце отрезка
9. Принимаем значение константы m.
10. Строим график функции mf¢ (x). Для всех х Î [1; 1, 5] функция mf¢ (x) удовлетворяет условию (67) (рис. 67).
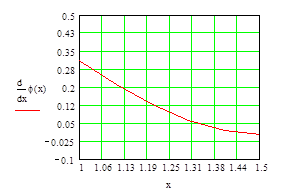
Рис. 67. График функции m× f¢ (x) на интервале [ a, b ] 11. Задаем еще раз функцию j(x) и получаем её вид, а также вид её производной в символьном виде с новым значением m. Строим график j¢ (x) (рис. 68). Теперь условие сходимости (64) выполняется.
Рис. 68. График функции j¢ (x) на интервале [ a, b ] при уточненном значении m 12. Будем искать точку пересечения функций j(x)=x- m× ( sin ( 2 x) - ln (x)) и g(x)=x (рис. 69).
Рис. 69. Поиск корня по функциям j (x) и g (х) 13. Теперь перейдем к уточнению корня методом итераций. Задаем степень точности решения и начальную точку.
14. Пишем программу согласно алгоритму рис. 61. Здесь используется бесконечный цикл, выход из которого осуществляется с помощью оператора break при достижении заданной степени точности. Результаты возвращаются в виде вектора z, их слияние осуществляется функцией stack.
15. Производим проверку решения (результат близок к нулю, следовательно, корень уравнения f(x)= 0 найден верно).
|













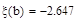 ,
,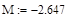 .
. ,
, .
.

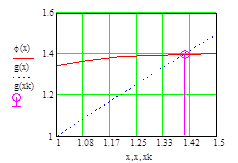

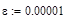



 Корень xk=1.399 найден за 4 итерации.
Корень xk=1.399 найден за 4 итерации.



