Приближенные методы решения систем линейных уравнений
7.3.4.1. Метод простых итераций Допустим, имеется система линейных алгебраических уравнений:
При решении этой системы точным методом корень получают сразу (x точн, y точн на рис. 44). При подстановке корня в исходную систему получают тождество. К приближенным методам относятся итерационные методы решения систем. При решении системы приближенным методом корень получают поэтапно, путем повторения ряда действий (итераций). Итерационным процессом называется повторяющийся процесс вычислений искомой величины по её значению на предыдущем шаге. Сначала задают начальное приближение (x 0, y 0), затем через эти значения находят следующую точку приближения к решению (x 1, y 1), через неё (x 2, y 2) и т. д. При подстановке полученного корня (x *, y *) в исходную систему получают приближенное равенство.
Рис. 44. Приближенное решение Для построения итерационных процессов решения линейных систем уравнений последние надо приводить к нормальному виду. Вид Если в правую часть системы, записанной в нормальном виде, подставить какое-либо значение вектора Полученную последовательность векторов Если последовательность сходится, т. е. имеет предел, то этот предел будет решением исходной системы уравнений. Для организации приближенного вычисления корней системы линейных уравнений необходимо выполнить следующие действия: 1) привести систему к нормальному виду; 2) определить условие сходимости последовательности 3) построить итерационный процесс; 4) определить достижение заданной степени точности решения, т. к. точное решение может быть получено при бесконечном итерационном процессе. Рассмотрим систему линейных уравнений 3-го порядка:
Нормальный вид системы (43):
Существует бесконечное множество способов приведения системы (43) к виду (44). Среди них всегда найдется такой, при котором будет выполняться условие сходимости итерационной последовательности Рассмотрим возможные варианты вычислений aij и bi на конкретном примере:
Вариант 1. Представим систему (45) в следующем виде:
или
где
Вариант 2. Для приведения системы к нормальному виду все члены левой части первого уравнения, кроме члена, содержащего а11, перенесем в правую часть и разделим уравнение на а11. Для второго уравнения все члены левой части перенесем также в правую часть, кроме члена, содержащего а22, и разделим уравнение на а22. Для третьего уравнения все члены левой части перенесем в правую часть, кроме члена, содержащего а33, и разделим уравнение на а33. Приведенная система будет иметь вид:
где
Условием сходимости последовательности
или (47)
то есть необходимо, чтобы сумма модулей коэффициентов нормальной системы уравнений по строкам или столбцам была меньше 1. Для построения итерационной процедуры необходимо выбрать первоначальное значение x1(0), x2(0), ¼;. Рекомендуется в качестве этих значений выбирать либо 0, либо значения свободных членов. Формульная запись метода простых итераций имеет вид:
В приближенных методах задается степень точности получения решения e (рис. 44). Условием достижения заданной степени точности является выполнение следующего неравенства:
Поскольку точное решение
Таким образом, условием нахождения вектора неизвестных является выполнение условия:
7.3.4.2. Метод Зейделя Другим вариантом итерационного процесса поиска корней системы линейных уравнений является метод Зейделя, который отличается от метода простых итераций тем, что при вычислении (i+ 1 ) -го приближения неизвестной величины xj учитываются уже полученные (i+ 1 ) -е приближения неизвестных x 1, x 2, ¼, xj- 1. Формульная запись метода имеет следующий вид:
где j= 2, 3, …, n; i= 0, 1, 2, …. Метод Зейделя обеспечивает более быструю сходимость к решению. Касаясь вопроса эффективности работы точных и приближенных методов, следует отметить, что на микроЭВМ, на которых обычно осуществляется решение задач АСУ ТП и память которых ограничена, использование точных методов для систем линейных уравнений выше 3-го порядка нерационально, так как их программная реализация занимает много памяти (обычно эти методы оформлены в виде стандартных программ). Для этих машин целесообразно использование реализующих численные методы простых программ, которые занимают немного места и быстро решаются.
|

 .
.
 называется каноническим видом, вид
называется каноническим видом, вид  – нормальным.
– нормальным.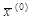 , то при известных значениях матриц L и
, то при известных значениях матриц L и  можно подсчитать новое значение
можно подсчитать новое значение  , подставить его снова в правую часть системы и т. д.
, подставить его снова в правую часть системы и т. д.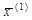 , ¼ называют итерационной последовательностью.
, ¼ называют итерационной последовательностью.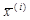 по коэффициентам системы, приведенной к нормальному виду;
по коэффициентам системы, приведенной к нормальному виду; (43)
(43) (44)
(44) , ¼ к соответствующему пределу.
, ¼ к соответствующему пределу.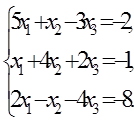 (45)
(45)
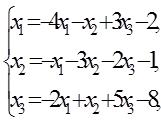

 (46)
(46)
 для всех
для всех 
 для всех
для всех 
 ,
,  (48)
(48) . (49)
. (49) . (50)
. (50) для всех
для всех 
 (51)
(51)


