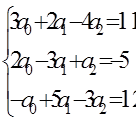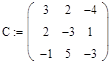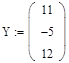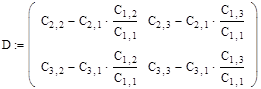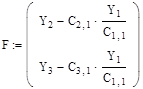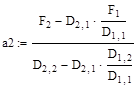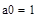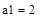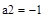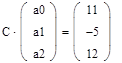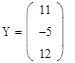Метод Гаусса

В основе метода Гаусса используются элементарные преобразования матрицы коэффициентов системы с целью приведения ее к более простому виду (например, треугольному), решение которой не представляет труда. В качестве таких преобразований используются:

а) вычитание из одной строки другой, умноженной на константу, отличную от нуля;

б) перестановка строк;

в) умножение строки на число, отличное от нуля.

Пусть имеется система линейных уравнений 3-го порядка:

и матрица коэффициентов системы не имеет нулевых диагональных элементов, и ее определитель отличен от нуля. Тогда решение может быть получено следующим образом.

1. Разделим все элементы первой строки на с ₁₁ (включая y):

2. Исключим элементы первого столбца из второго и третьего уравнений системы (элементы c₂₁ и c₃₁). Для этого элементы первой строки умножим на c₂₁ и c₃₁, т. е. получим:

и

3. Затем из элементов второй и третьей строки вычтем соответствующие элементы полученных уравнений, т. е.

Введем переобозначение для второго и третьего уравнений системы:

,

где , , ,

, , .

4. Вновь полученную вторую строку разделим на d ₁₁:

5. Исключим элемент d ₂₁ из третьей строки. Для этого элементы второй строки умножим на d ₂₁:

.

6. Затем из элементов третьей строки вычтем элементы полученного уравнения.

7. Из последнего уравнения найдем a ₂, из второго a ₁ и из первого – a ₀.

,

,

.

Пример решения системы линейных алгебраических уравнений методом Гаусса.

Имеем систему (32):

1. Зададим системную переменную, исходные значения матрицы системы и вектора свободных членов

2. Сформируем промежуточные матрицы для переобозначения:

3. Решим систему и высветим результат:

4. Осуществим проверку решения:

Результаты совпали, следовательно, решение верно.
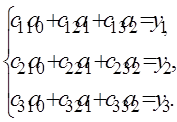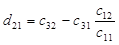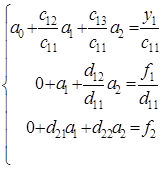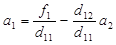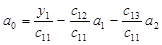