Аппроксимация с использованием метода выбранных точек

Запрограммируем в Mathcad решение примера, описываемого зависимостью (15).

1. Задаем системной переменной значение 1.

2. Задаем количество экспериментальных точек и ранжированную переменную

3. Задаем значения экспериментальных массивов и констант.

4. Задаем 3 произвольные точки (укажем их индексы):

5. Формируем главную матрицу системы уравнений:

6. Формируем вектор свободных членов:

7. Решаем полученную систему линейных уравнений методом Крамера:

Составляем матрицы

Рассчитываем определители

Находим неизвестные коэффициенты:

Внимание! В примере определители рассчитываются с использованием встроенной функции. При расчете собственного задания студент должен запрограммировать расчет определителей самостоятельно, как в лабораторной работе № 1, а встроенные функции использовать для проверки.

_8. Рассчитываем коэффициент a₀

9. Находим расчетные значения функции:

и высвечиваем результаты

10. Строим экспериментальный и расчетный графики (рис. 30)

Рис. 30. Результаты аппроксимации методом выбранных точек

(набор точек №1)

11. Находим максимальный и минимальный элемент экспериментального массива

12. Рассчитываем погрешность, %:

13. Выбираем другие 3 точки:

14. Повторяем пункты 5–8. Находим расчетные значения функции и высвечиваем результаты:

15. Рассчитываем погрешность, %:

,

.

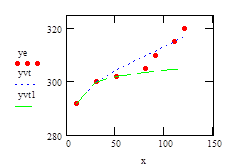
16. Строим экспериментальный и расчетные графики, полученные для первого и второго набора точек (рис. 31).

Рис. 31. Результаты аппроксимации методом выбранных точек

(набор точек № 2)

Анализ результатов показывает, что результаты аппроксимации с помощью метода выбранных точек существенно зависят от того, какие точки были выбраны. Кроме того, расчетная кривая обязательно проходит через выбранные экспериментальные точки.
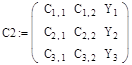
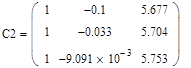
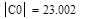
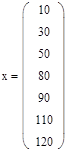