Метод наименьших квадратов. Параметры a1, a2 ¼ , ak аппроксимирующей зависимости (12) находятся, исходя из следующего условия(сумма квадратов невязок между экспериментальными и
Параметры a1, a2 ¼, ak аппроксимирующей зависимости (12) находятся, исходя из следующего условия (сумма квадратов невязок между экспериментальными и расчетными данными на всем интервале аппроксимации должна быть минимальна, рис. 29):
где yiэ – экспериментальные данные;
i – порядковый номер точки; m – число экспериментальных точек.
Рис. 29. Метод наименьших квадратов (ye – экспериментальные данные, ymnk – расчетные данные) Поскольку критерий R(a1, а2, ¼, ak) является функцией неизвестных параметров, его использование позволяет получить из условия (21) систему уравнений, в которой число неизвестных равно числу уравнений. Условием существования экстремума (в нашем случае минимума) функции нескольких переменных является равенство нулю частных производных по каждой из переменных. Поэтому для приведения системы (21) к виду, удобному для решения, необходимо найти частные производные функции R по каждой из переменных a1, а2, ¼, ak:
Коэффициенты зависимости (12) получают в результате решения системы уравнений (22). Для примера выберем ту же зависимость (13)
Необходимо найти неизвестные параметры a0, a1, a2. Для этого запишем условие (21):
и вычислим частные производные:
преобразуем:
Решение полученной системы уравнений (22) относительно неизвестных параметров a0, a1, a2 позволяет найти параметры аппроксимирующей зависимости. Рассмотрим применение метода наименьших квадратов для нахождения параметров зависимости (15)
Как и в предыдущем методе, приведем зависимость (15) к линейному виду относительно неизвестных коэффициентов:
Тогда вместо зависимости (21)
в качестве условия поиска коэффициентов используем
или
Вычислим частные производные
преобразуем:
Решим систему (24) относительно А0 a1, a2 и рассчитаем коэффициент а0:
|

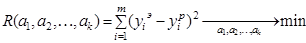 , (21)
, (21)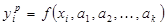 – расчетные данные;
– расчетные данные;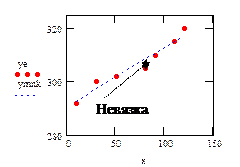
 . (22)
. (22)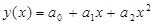 .
.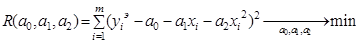
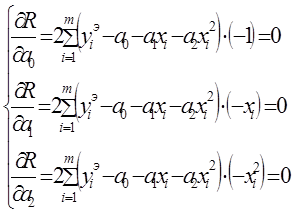 ,
,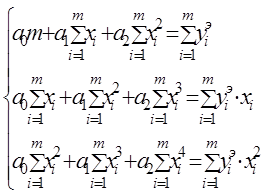 . (22)
. (22)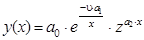 .
. .
.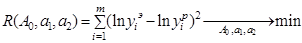
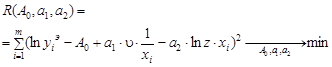 (23)
(23)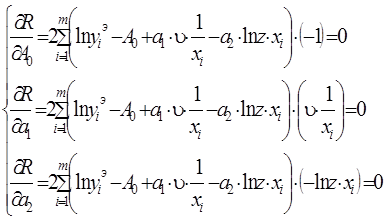
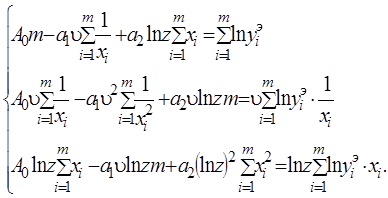 (24)
(24)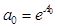 .
.


