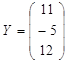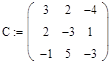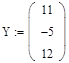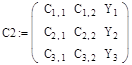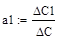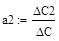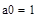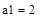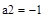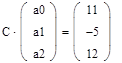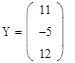Метод КрамераПусть имеется система уравнений 3-го порядка
где
или в матричном виде СA=Y, где C – матрица коэффициентов системы; A – вектор неизвестных; Y – вектор правых частей. Согласно теореме Крамера, решение (30) может быть найдено из формулы:
где Ci – матрица C, у которой i -й столбец заменен вектором свободных членов – вектором Y. Т. е.
Найдем определители матриц С, С0, С1, С2.
В Mathcad существует встроенная функция для расчета определителя матрицы. Она вызывается нажатием кнопки Determinant (Вычисление определителя) на панели Matrix (Матрицы) (рис. 40).
Рис. 40. Вызов вычисления определителя матрицы Зная определители, найдем a0, a1, a2.
Пример решения системы линейных алгебраических уравнений методом Крамера. Запрограммируем в Mathcad процесс решения системы методом Крамера. Имеем систему:
Запишем систему (32) в матричном виде:
С× a=Y. 1. Зададим системную переменную
2. Зададим исходные значения матрицы системы и вектора свободных членов
3. Сформируем ещё три матрицы
4. Рассчитаем определитель матрицы С
5. Проверим правильность расчета с помощью встроенной функции Mathcad
6. Рассчитаем остальные определители и проводим проверку правильности расчета. 7. Найдем решение системы и высвечиваем результат
8. Осуществим проверку решения системы
Результаты совпали, следовательно, решение верно.
|
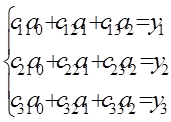, (30)
, 
, 
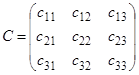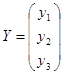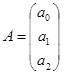
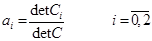, (31)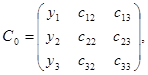
, 
, 
.
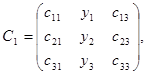
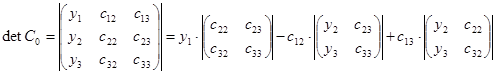
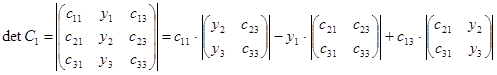
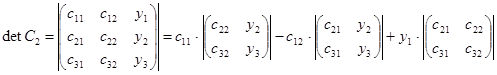
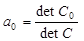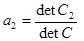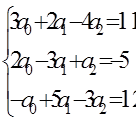(32)
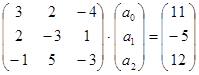или при вводе обозначений
, 
, 
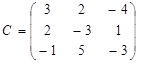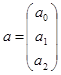